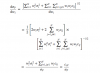Hi
I'm somewhat confused between Marginal and Incremental VAR. Am i right to say that the only difference between the two is that Incremental VAR is calculated precisely from a total revaluation of the portfolio and that Marginal VAR is just an estimation of the change in VAR?
Regards
I'm somewhat confused between Marginal and Incremental VAR. Am i right to say that the only difference between the two is that Incremental VAR is calculated precisely from a total revaluation of the portfolio and that Marginal VAR is just an estimation of the change in VAR?
Regards