Difference between Marginal and incremental VAR
- Thread starter CYLoh
- Start date
You solve for rho since portfolio SD is given:
EDIT: I am actually getting a correlation of .5126
Last edited:
@Ali Ehsan Abbas I used the formula to which @bpdulog refers such that sqrt[(140/300)^2*0.20^2 + (160/300)^2*0.12^2 + 2*(140/300)*(160/300)*0.20*0.120*0.50] = 13.7042%. If I uses sovler, ρ = 0.499042585684933, so I think they were assuming 0.50 
Thanks!
Thanks!@David Harper CFA FRM
The reading says both incremental and component VaR refers to the change in VaR due to deletion of a position/component. So what exactly is the difference between Incremental and Component VaR?
emilioalzamora1
Well-Known Member
I don't quite understand why every single piece (in particular qualitative stuff) needs to be explained. There is a vast amount of literature where you can get the information/proof yourself. And this is sth. which is the minimum what can be expected from a well rounded candidate.
Component VaR (CVaR): it is simply the marginal VaR times the wealth (W) invested in a particular asset and shows how the portfolio VaR would change if the component was deleted from the portfolio. Porfolio volatility changes in a non-linear fashion due to different underlying components which drive the portfolio volatility (VaR). Component VaR is only useful when we have 1.) a large portfolio (high level of wealth invested) and 2.) having small individual positions (components). This ensures that the portfolio VaR changes more or less (approx.) proprionately if a component would be deleted from the portfolio.
CVaR can be sort of interpreted as risk measure to reflect correlations because part of the CVaR calculation (formula) depends on the correl coefficient. Having a negative correl and therefore a negative beta, the position acts a hedge against higher portfolio VaR (in other words, it has a positive effect yielding to lower portfolio VaR).
Remember:
CVaR(asset A) = alpha * sigma(p) * W(A) * beta(A) = CVaR(A)/VaR(p) = w(a) * beta(A)
where the two on the right-hand side, yield the %-contribution of Asset(A) to total Portfolio VaR
1. CVaR(A)/VaR(p)
2. w(a) * beta(A)
1. CVaR(asset A) = alpha * sigma(p) * W(A) * beta(A)
OR in %-terms of the portfolio VaR
1. CVaR(asset A) = CVaR(A)/VaR(p)
2. CVaR(asset A) = w(a) * beta(A)
Incremental VaR: change in the portfolio VaR due to adding a new position. In contrast to the component VaR it is also applicable for large positions. @David Harper CFA FRM do you agree with this?
In case of a large position, the portfolio VaR changes in non-linear fashion and IVaR is the better measure compared to the CVaR.
Put differently, IVaR is deemed to be more accurate when dealing with large (changes in) positions than the component VaR but comes with the drawback of doing a full revaluation (computionally burdensome).
We can achieve the approx. same result using either Marginal VaR or incremental VaR (but only if the change in the position is small. Let's say you are invested in 2Million JPY and increase the position by JPY 10,000).
Notice:
Component VaR has an important limitation: it is a linear marginal analysis. The component risks add up to total VaR because of linear homogeneity working through Euler’s theorem, but the price we pay for this additivity property is that we have to assume that each component VaR is simply the position size multiplied by the marginal VaR. This is restrictive because it implies
that the component VaR is proportional to the position size: if we change the size of the position by k%, then the component VaR will also change by k%. Strictly speaking, this linear
proportionality is only guaranteed if each position is very small relative to the total portfolio; and where the position size is significant relative to the total portfolio, then the component VaR estimated in this way is likely, at best, to give only an approximate idea of the impact of the position on the portfolio VaR. If we want a ‘true’ estimate, we would have to resort
to the IVaR, and take the difference between the VaRs of the portfolio with and without the position concerned. The IVaR then gives us an exact estimate of the impact of the portfolio.
Unfortunately, this exactness has its price: we lose the additivity property, and the component VaRs no longer add up to equal the total VaR, which makes it difficult to interpret these IVaRs
(or CVaRs or whatever else we call them) as true decompositions of the total risk. In short, when positions are significant in size relative to the total portfolio, we can only hope for our
CVaRs to give approximate estimates of the effects of the positions concerned on the portfolio VaR.
Component VaR (CVaR): it is simply the marginal VaR times the wealth (W) invested in a particular asset and shows how the portfolio VaR would change if the component was deleted from the portfolio. Porfolio volatility changes in a non-linear fashion due to different underlying components which drive the portfolio volatility (VaR). Component VaR is only useful when we have 1.) a large portfolio (high level of wealth invested) and 2.) having small individual positions (components). This ensures that the portfolio VaR changes more or less (approx.) proprionately if a component would be deleted from the portfolio.
CVaR can be sort of interpreted as risk measure to reflect correlations because part of the CVaR calculation (formula) depends on the correl coefficient. Having a negative correl and therefore a negative beta, the position acts a hedge against higher portfolio VaR (in other words, it has a positive effect yielding to lower portfolio VaR).
Remember:
CVaR(asset A) = alpha * sigma(p) * W(A) * beta(A) = CVaR(A)/VaR(p) = w(a) * beta(A)
where the two on the right-hand side, yield the %-contribution of Asset(A) to total Portfolio VaR
1. CVaR(A)/VaR(p)
2. w(a) * beta(A)
- alpha denotes the z-value (will either be 1,65 at 95% or 2,33 at 99%)
- sigma (p) stands for portfolio volatility
- W(A) stands for total $wealth
- w(a) stands for %-weight of Asset(A)
1. CVaR(asset A) = alpha * sigma(p) * W(A) * beta(A)
OR in %-terms of the portfolio VaR
1. CVaR(asset A) = CVaR(A)/VaR(p)
2. CVaR(asset A) = w(a) * beta(A)
Incremental VaR: change in the portfolio VaR due to adding a new position. In contrast to the component VaR it is also applicable for large positions. @David Harper CFA FRM do you agree with this?
In case of a large position, the portfolio VaR changes in non-linear fashion and IVaR is the better measure compared to the CVaR.
Put differently, IVaR is deemed to be more accurate when dealing with large (changes in) positions than the component VaR but comes with the drawback of doing a full revaluation (computionally burdensome).
We can achieve the approx. same result using either Marginal VaR or incremental VaR (but only if the change in the position is small. Let's say you are invested in 2Million JPY and increase the position by JPY 10,000).
Notice:
- the marginal VaR is always very small in number (it only measures the tiny little change) whereas the component VaR is always big relative to the marginal VaR (the individual components of the portfolio should add up to the portfolio VaR approximately!) as the component VaR is the marginal VaR times the total wealth invested in asset (A)
- the component VaR can be written in %-form where we first need to determine the beta of the asset and then can write: component VaR = beta (asset A) * weight (in% of asset A)
Component VaR has an important limitation: it is a linear marginal analysis. The component risks add up to total VaR because of linear homogeneity working through Euler’s theorem, but the price we pay for this additivity property is that we have to assume that each component VaR is simply the position size multiplied by the marginal VaR. This is restrictive because it implies
that the component VaR is proportional to the position size: if we change the size of the position by k%, then the component VaR will also change by k%. Strictly speaking, this linear
proportionality is only guaranteed if each position is very small relative to the total portfolio; and where the position size is significant relative to the total portfolio, then the component VaR estimated in this way is likely, at best, to give only an approximate idea of the impact of the position on the portfolio VaR. If we want a ‘true’ estimate, we would have to resort
to the IVaR, and take the difference between the VaRs of the portfolio with and without the position concerned. The IVaR then gives us an exact estimate of the impact of the portfolio.
Unfortunately, this exactness has its price: we lose the additivity property, and the component VaRs no longer add up to equal the total VaR, which makes it difficult to interpret these IVaRs
(or CVaRs or whatever else we call them) as true decompositions of the total risk. In short, when positions are significant in size relative to the total portfolio, we can only hope for our
CVaRs to give approximate estimates of the effects of the positions concerned on the portfolio VaR.
Last edited:
@emilioalzamora1
All these concepts I have read at many places. But a little ambiguity still remains.
My entire point of asking this was if a question is asked that 'if we delete a position from the portfolio, what impact will it have on VaR?'
By definition the answer should be Component VaR of that position but at majority places Incremental VaR is used to answer such a question.
So which approach should be followed and why?
All these concepts I have read at many places. But a little ambiguity still remains.
My entire point of asking this was if a question is asked that 'if we delete a position from the portfolio, what impact will it have on VaR?'
By definition the answer should be Component VaR of that position but at majority places Incremental VaR is used to answer such a question.
So which approach should be followed and why?
emilioalzamora1
Well-Known Member
I don't understand your question and what you are referring here?
If you delete ANY position from the portfolio, then the portfolio VaR will go down (except the position has zero risk, then the portfolio VaR will remain the same) where the amount (magnitude) of how much the portfolio VaR is reduced depends on the risk characteristics (vol, beta) and it's (Wealth) of the indivudal position which is deleted.
The above describes the opposite of the subadditivity principle (which means that aggregating individual risk positions they will diversify risk or in the worst case NOT increase risk: the risk of the sum of portfolio positions (riks) is always less than or equal to the individual positions (risks).
If you delete ANY position from the portfolio, then the portfolio VaR will go down (except the position has zero risk, then the portfolio VaR will remain the same) where the amount (magnitude) of how much the portfolio VaR is reduced depends on the risk characteristics (vol, beta) and it's (Wealth) of the indivudal position which is deleted.
The above describes the opposite of the subadditivity principle (which means that aggregating individual risk positions they will diversify risk or in the worst case NOT increase risk: the risk of the sum of portfolio positions (riks) is always less than or equal to the individual positions (risks).
Last edited:
My question is
Say a portfolio contains 3 assets namely X, Y and Z. It has a portfolio VaR of 'some' amount and the weights as well as marginal VaR of each position is given. Now the question asks that if Asset Y is deleted from the portfolio what will be its impact on the portfolio VaR , in other words by how much will the portfolio VaR change due to deletion of this position?
What I wanted to know is that will this change be equal to Y's Component VaR or Incremental VaR because by definition the answer should be Component VaR of that position but at majority places Incremental VaR is used to answer such a question.
So which approach should be followed and why?
@David Harper CFA FRM if you could put some light on this.
Say a portfolio contains 3 assets namely X, Y and Z. It has a portfolio VaR of 'some' amount and the weights as well as marginal VaR of each position is given. Now the question asks that if Asset Y is deleted from the portfolio what will be its impact on the portfolio VaR , in other words by how much will the portfolio VaR change due to deletion of this position?
What I wanted to know is that will this change be equal to Y's Component VaR or Incremental VaR because by definition the answer should be Component VaR of that position but at majority places Incremental VaR is used to answer such a question.
So which approach should be followed and why?
@David Harper CFA FRM if you could put some light on this.
emilioalzamora1
Well-Known Member
The question (if you read through my explanations) should be self-explanatory. If you delete a complete position (Y) from the portfolio, only IVaR is useful because component VaR is only applicable for small changes (let's say the position of Y - the wealth invested in Y - is reduced by small amount, say 1%).
Okay Thanks @emilioalzamora1 got my answer
But about what you mentioned if say wealth invested in Y is decreased by 1%, how will we go about it
Lets assume that Portfolion VaR is $9 Million, and Y's Component VaR is $3.5Mn
So will the answer be 1% of 3.5mn?
In short, then how will the component VaR be used?
But about what you mentioned if say wealth invested in Y is decreased by 1%, how will we go about it
Lets assume that Portfolion VaR is $9 Million, and Y's Component VaR is $3.5Mn
So will the answer be 1% of 3.5mn?
In short, then how will the component VaR be used?
emilioalzamora1
Well-Known Member
No, it is not that easy! I just used this 1% example to highlight the fact that Component VaR is only applicable in case of a very minor/small change in the position of (let's say asset Y). Imagine you are invested with 10M in the JPY and reduce or increase your holding by 1% (having 10M*0.01 = 100,000). In this case an approx. linear change in portfolio VaR is justified whereas for a major change in your holding by 70% is not and component VaR does not longer give yield accurate results.
This is simply an example to differentiate between component vs. incremental VaR but NOT the component VaR itself. Please see the formulae given in Jorion 'Value at Risk' and all the contributions here in the forum about the calculation.
This is simply an example to differentiate between component vs. incremental VaR but NOT the component VaR itself. Please see the formulae given in Jorion 'Value at Risk' and all the contributions here in the forum about the calculation.
Just to add to @emilioalzamora1 's explanation, I think Jorion's figure 7-4 may be helpful (see below, it plots the example in Chapter 7). The X-axis represents the position held in one of the assets (Canadian dollars, CAD) where the current CAD position is $1.0 million; the vertical axis is the portfolio VaR which is currently ~ 258,000 (the upper horizontal line). The key line maybe is the bold non-linear plot of the true (accurate) portfolio VaR; as the CAD position is reduced, portfolio VaR decreases but non-linearly. Notice how Jorion compares the Component VaR with Incremental VaR? Consistent with @emilioalzamora1 's post above, Component VaR is informed by (scaled by the unitless) marginal VaR (marginal VaR is the slope of the tangent line at X = $1.0 mm), which itself is a first partial derivative. So the component VaR is a linear approximation of the accurate incremental VaR under the assumption that incremental VaR is measuring a full exit of the position. Also, Incremental VaR is a "simulation" (repricing portfolio VaR after subtracting the position), while Component VaR is an analytic.
The other thing I would add is that neither requires subtraction of the entire position. Component VaR is an estimate of the reduction in VaR due to a total exit of the position, but as shown below, it is likely to be inaccurate, and it merely equal to marginal VaR * $Position. So it estimates any position change. For example, if we want to reduce portfolio VaR by X$, then we can estimate the Δposition with [portfolio VaR change desired]/MVaR. And this, in turn, would be approximating the actual incremental VaR due to a Δposition. I hope that's additive!
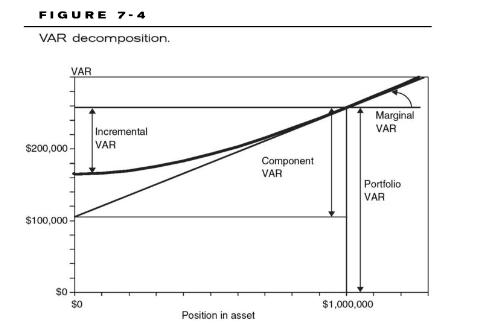
The other thing I would add is that neither requires subtraction of the entire position. Component VaR is an estimate of the reduction in VaR due to a total exit of the position, but as shown below, it is likely to be inaccurate, and it merely equal to marginal VaR * $Position. So it estimates any position change. For example, if we want to reduce portfolio VaR by X$, then we can estimate the Δposition with [portfolio VaR change desired]/MVaR. And this, in turn, would be approximating the actual incremental VaR due to a Δposition. I hope that's additive!
Last edited:
emilioalzamora1
Well-Known Member
Superb, @David Harper CFA FRM! Thanks.
WhizzKidd
Member
Hi @David Harper CFA FRM
Just wondering about this (what do you think):
Say, an index halted trading for 5 weeks, during that 5 week, would the VaR of a portfolio replicating the index be 0 or unchanged from before the halt in trading?
Is it correct in saying here, that VaR cannot be zero, so either unchanged or lower?
Then later would the VaR just after trading has started again now be higher, unchanged or lower?
This would also be lower, as the 25 trading day period is used in the VaR calc?
Just wondering about this (what do you think):
Say, an index halted trading for 5 weeks, during that 5 week, would the VaR of a portfolio replicating the index be 0 or unchanged from before the halt in trading?
Is it correct in saying here, that VaR cannot be zero, so either unchanged or lower?
Then later would the VaR just after trading has started again now be higher, unchanged or lower?
This would also be lower, as the 25 trading day period is used in the VaR calc?
Srilakshmi
Member
Is the beta given in the question with respect to the portfolio? If so, should the beta of the portfolio with respect to itself should be 1 right?
@Srilakshmi yes, exactly. That's why this table in Q60 cannot be correct. The marginal VaR of HIJ is informed by β(HIJ, Portfolio) such that, while the β(HIJ) + β(KLM) <> 1.0, it nevertheless should show portfolio beta of 1.0 to reflect that all three betas are with respect to the portfolio.
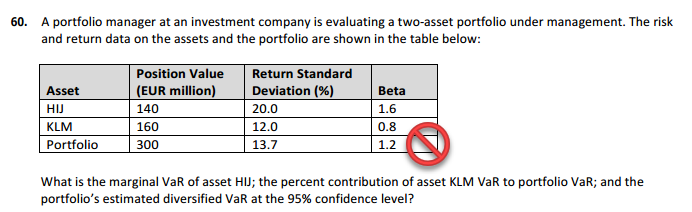
Dear David,@Srilakshmi yes, exactly. That's why this table in Q60 cannot be correct. The marginal VaR of HIJ is informed by β(HIJ, Portfolio) such that, while the β(HIJ) + β(KLM) <> 1.0, it nevertheless should show portfolio beta of 1.0 to reflect that all three betas are with respect to the portfolio.
what was the GARP feedback about this question that the betas are not internally consistent? will they consider this issue in FRM exam? and why they don't publish a correction to this question?
Finally, the sum of weighted betas should equal 1.0. For example 140/300 * B(HIJ) + 160/300*B(KLM) = 1.0. This can be used as a check !!
Regards,
Jamal
@GARP2015
I'm not sure if @David Harper CFA FRM received anything further on this, but this is the response that we received from GARP regarding this question:
"Regarding Q60 in the Part II Practice Exam, we will be putting out a revised version of that question soon that should address the issue of consistency amongst the inputs numbers, calculations, and outputs."
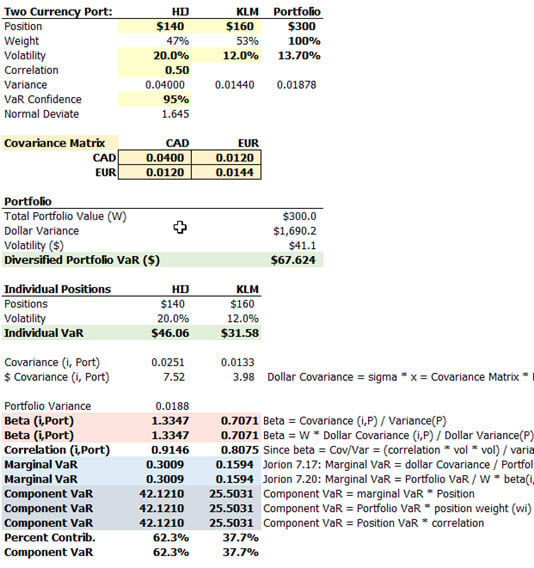
Thank you @Nicole Seaman that is exactly the relevant email: we only received it this week. We've been driving this point for years actually, so I am very happy to report that GARP finally understands the importance of a correctly specified portfolio VaR. Jamal (@GARP2015 ) you are exactly correct about an easy test for the betas; below is the specification that I sent GARP for this question. Notice that indeed (140/300) * 1.3347 + (160/1300) * 0.7071 = 1.00. Thank you!
Similar threads
