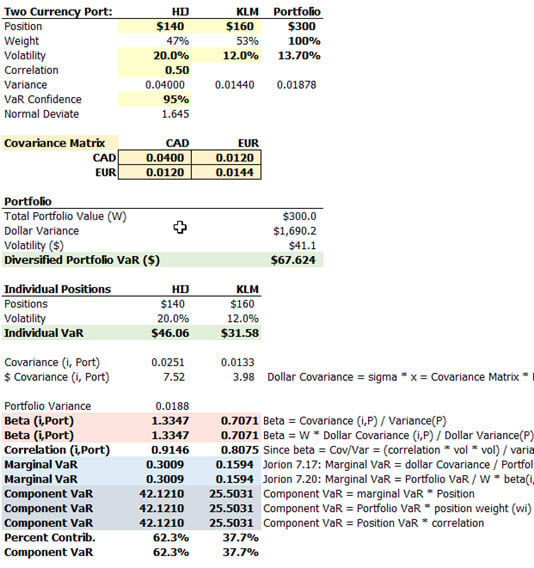
Thanks David, I appreciate your response.Thank you @Nicole Seaman that is exactly the relevant email: we only received it this week. We've been driving this point for years actually, so I am very happy to report that GARP finally understands the importance of a correctly specified portfolio VaR. Jamal (@GARP2015 ) you are exactly correct about an easy test for the betas; below is the specification that I sent GARP for this question. Notice that indeed (140/300) * 1.3347 + (160/1300) * 0.7071 = 1.00. Thank you!
Actually, I have found the same inconsistency in 2010 practice exam and maybe more in other years, so since 2010 GARP are publishing wrong questions.
How many candidates failed FRM because of these questions? Remember that FRM practice questions are old real exams !!!
Finally, one more way to calculate component VaR contribution=(Beta*weight * Portfolio VaR), then you can calculate Marginal VaR by dividing CVaR over position value. In the example above and using correct Betas, Component Contribution of HIJ = 1.337 * 140/300 = 62.3%, the CVaR = 62.3%* 67.62 = 42.19, MVaR = 42.18/140 = 0.30.
It is easier to start with Beta ...
Jamal

 about the low standard that has historically been employed on the portfolio VaR questions; I have supplied GARP with the correct approach to internal consistency many many times. It is very disappointing to me personally, especially given that it takes hard work to master these concepts. Candidates, who invest significantly their time and money, deserve correctly specified questions.
about the low standard that has historically been employed on the portfolio VaR questions; I have supplied GARP with the correct approach to internal consistency many many times. It is very disappointing to me personally, especially given that it takes hard work to master these concepts. Candidates, who invest significantly their time and money, deserve correctly specified questions.