gargi.adhikari
Active Member
Hi,
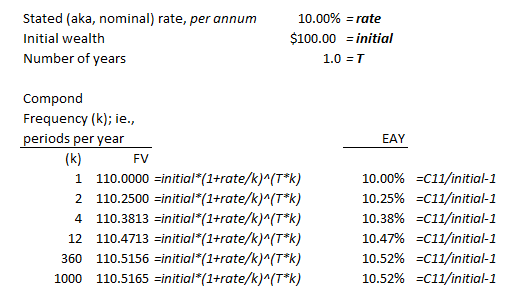
In reference to TUCKMAN CHAPTER 2 ( Pg 16):-
I circled back to Tuckman Chapter 2 to double check I covered everything and something caught my eye which I could not reason and I think again there might be a gap in my understanding which is why I am posting this question...
Want to start by saying that, I understand how we derived/calculated the Discrete and Continuous rates for the different Compounding frequencies. However, I am having trouble with the numbers circled in pink.
I tried deriving the FVs/Terminal Values by plugging in the Rm values: PV( 1 + Rm/m)^mT
PV=100, Rm= 9.7618%, m=2 , T= 1 yr. So the FV for Compounding Freq= 2 should be = 100 ( 1+ .097618/2)^2.1 =110.0000318
Similarly, all the other FVs/Terminal Values circled in pink are a bit off...what am I missing here ...
Please help


In reference to TUCKMAN CHAPTER 2 ( Pg 16):-
I circled back to Tuckman Chapter 2 to double check I covered everything and something caught my eye which I could not reason and I think again there might be a gap in my understanding which is why I am posting this question...
Want to start by saying that, I understand how we derived/calculated the Discrete and Continuous rates for the different Compounding frequencies. However, I am having trouble with the numbers circled in pink.
I tried deriving the FVs/Terminal Values by plugging in the Rm values: PV( 1 + Rm/m)^mT
PV=100, Rm= 9.7618%, m=2 , T= 1 yr. So the FV for Compounding Freq= 2 should be = 100 ( 1+ .097618/2)^2.1 =110.0000318
Similarly, all the other FVs/Terminal Values circled in pink are a bit off...what am I missing here ...

Please help




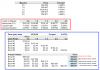
 but...unfortunately ...I still don't see how you're deriving Col I.
but...unfortunately ...I still don't see how you're deriving Col I.