gargi.adhikari
Active Member
In reference to R19.P1.T3.FIN_PRODS_HULL_Ch5_Cash_Or_Carry_Learning_Spreadsheet:-
In the Associated Learning Spreadsheet to illustrate the Cash and Carry Model, tab 3b.4 Hull_Ch5 (COC):
For the Col F- Hull Example- 10 Month Forward On Stock with 3 Dividends, How are we calculating the PV of Income=$ 2.16.....? Where are we getting the .75 from in the formula...? Is that = the FV of Dividend for each period...? Am not seeing any value in Dividends....
Also, Col G-Hull Long Forward On Asset Paying Lumpsum Income , How are we getting the formula for the Yield/Dividend = (2*LN(1+4%/2))/12
:-(
Grateful for any insight into this ...
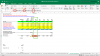
In the Associated Learning Spreadsheet to illustrate the Cash and Carry Model, tab 3b.4 Hull_Ch5 (COC):
For the Col F- Hull Example- 10 Month Forward On Stock with 3 Dividends, How are we calculating the PV of Income=$ 2.16.....? Where are we getting the .75 from in the formula...? Is that = the FV of Dividend for each period...? Am not seeing any value in Dividends....
Also, Col G-Hull Long Forward On Asset Paying Lumpsum Income , How are we getting the formula for the Yield/Dividend = (2*LN(1+4%/2))/12
:-(
Grateful for any insight into this ...

Last edited:



 in a sincere attempt to understand the spreadsheet and the calculations. Sooner or later it will benefit somebody else, and it helps me improve the spreadsheet for better readability when I update it. It's all good. Thanks!
in a sincere attempt to understand the spreadsheet and the calculations. Sooner or later it will benefit somebody else, and it helps me improve the spreadsheet for better readability when I update it. It's all good. Thanks!