I will post here selected observations made (either by myself or subscribers/members) about the newest material. As most already know, the entire Part 1 FRM has experienced a big change, but the change can be deceiving in appearance because as I replied over on the reddit FRM board, with respect just to Part 1, the Part 1 learning objectives (LOs) are mostly unchanged. Rather, what changed is that GARP replaced the previous source material (an anthology of external authors) with their own internal content. However, most of the new GARP content maps directly (1:1) to previously assigned chapters. For this reason, the change appears big, but it actually small if your question is "In terms only of what I need to know for the exam, what is different in Part 1?" (Answer: not much is greatly different). Further, given this is GARP's first year, we should not expect anything near perfection in their material (put another way, it's GARP' first edition. The Hull chapters from last year, for example, had ten editions and many years of refinement/corrections).
For starters:
For starters:
- [FRM-1 Foundations] The text reads "expected shortfall (ES), which is a statistical measure designed to quantify the mean risk in the tail of the distribution beyond the cut-off of the VaR measure." and EOC Question 1.25 reinforces as a TRUE statement that "ES is a statistical measure designed to quantify the mean risk in the tail of the distribution beyond the cut-off of the VaR measure." But this refers to the conditional VaR or tail conditional expectation (TCE) by confusing a quantile-threshold with a probability-threshold.
- From my perspective, this should instead read something like (emphasis mine) "expected shortfall (ES), which is a statistical measure designed to quantify the mean risk in the tail of the distribution beyond the selected probability (or confidence) threshold"
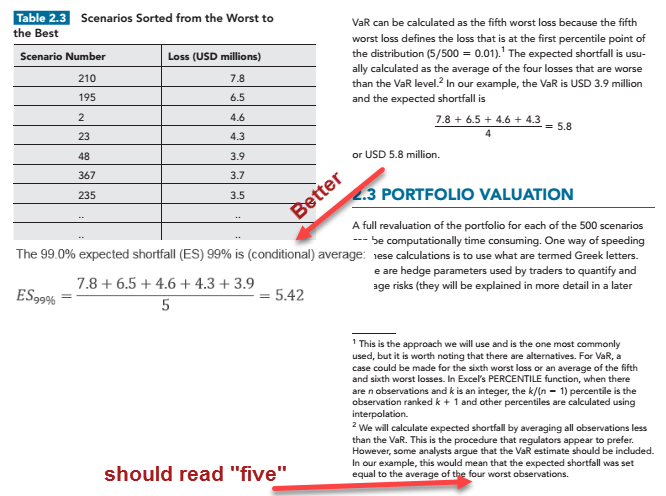
- Why does it matter? Because we know quantile-threshold definition causes confusion (for example) when confronting test questions. If the distribution is discrete, VaR is ambiguous. Here is a super-simple example: What is the 95.0% basic HS VaR when the super-tiny window is only n = 20 and given in L(+)/P(-) = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}. Strictly, the best answer is the (20*5%+1)th = 2nd worst loss, or 19. However, Jorion would say 20, and 19.5 is valid. Three fine answers (Excel will give you two more: there are probably fully five good answers!). That is, VaR is here ambiguous. If we define ES in terms of VaR (which is a quantile-threshold), then an ES defined in terms of the VaR is often also ambiguous. But we don't do that. We define ES in terms of probability-threshold, which is never ambiguous. If you think your ES has more than one answer, you are defining ES incorrectly. The 95% ES is the conditional mean: the weighted-average of the 5% (1 - 95%) loss tail. This forum has tons of discussion on this, and a more thorough explanation can be found on page 35 of Dowd's classic Measuring Market Risk (section 2.3.2).
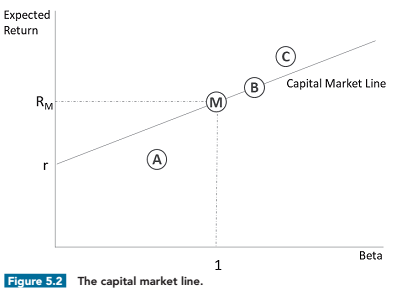
- [FRM-5 Foundations] The text goofs the CML saying, "Figure 5.2 shows the capital market line, defined as the linear relationship between the expected rate of return and systematic risk." However, is the security market line (SML) that plots return against beta; aka, systematic risk; the capital market line (CML) plots against standard deviation (aka, total risk, volatility). I have a video on this topic here https://forum.bionicturtle.com/thre...ne-cml-versus-security-market-line-sml.21443/
- [QA Chapter 8: Regression with Multiple Explanatory Variables] Credit to @jimmykaw who observes apparent typo on page 127, such that text probably should read:
"As explained previously, adding an additional explanatory variable usually increases R2 (because it decreases RSS) and can never decrease it. On the other hand, including additional explanatory variables (i.e., increasing k) always increases ξ. The adjusted R2 captures the tradeoff between increasing ξ and decreasing RSS as one considers larger models. If a model with additional explanatory variables produces a negligible decrease in the RSS when compared to a base model, then the loss of a degree of freedom produces a smaller R2." -- 2020 Financial Risk Management Part I: Quantitative Analysis, 10th Edition. Pearson Learning Solutions, 10/2019
- [VRM-1 Learning objective] This is incorrect: "Describe spectral risk measures and explain how VaR and ES are special cases of spectral risk measures." Value at Risk (VaR) is not (a special case of) a spectral measure because it is a dirac delta function that violates the non-negativity weighting function requirement of a spectral. VaR and ES are special cases of the general risk measure; but only ES is spectral and coherent, but VaR is neither. Effectively the general risk measure is spectral if and only if (iif) it is coherent.
As replacement, I proposed either of the following two correct statements:- "Describe spectral risk measures and explain how VaR and ES are special cases of the general risk measure." or also plausible:
- "Describe spectral risk measures and explain how ES is spectral but VaR is not spectral (even as both are special cases of the general risk measure)."
Last edited:




 (I think religions can take symbols seriously, but as an aspiring mathematician I don't think mathematical symbols can be religious!) The above is actually how Kevin Dowd defines VaR, he signifies the confidence level with α, and his significance level is 1 - α = p. (Is he your source?). So, if we do have α = 5.0% such that p = 95.0%, we can express VaR either as:
(I think religions can take symbols seriously, but as an aspiring mathematician I don't think mathematical symbols can be religious!) The above is actually how Kevin Dowd defines VaR, he signifies the confidence level with α, and his significance level is 1 - α = p. (Is he your source?). So, if we do have α = 5.0% such that p = 95.0%, we can express VaR either as: