Probability - Conditional Independence

[Raj Sachdeva]

@David Harper CFA FRM , can you please share an example of the below case if possible?

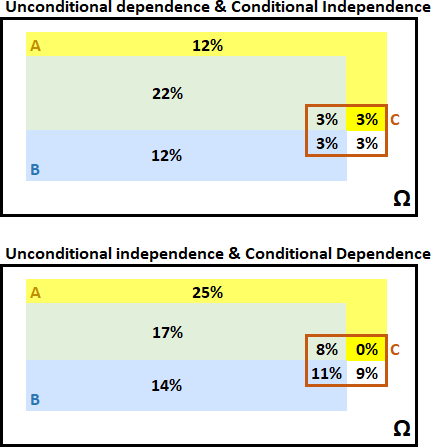
Events can be conditionally independent yet unconditionally dependent. Events can be conditionally dependent, yet independent! [Chapter 1: Fundamentals of Probability, Study Notes, Pg. 5]

It will be easy to remember this with an example.

Thanks,
Raj

 

[David Harper CFA FRM]

Hi @Raj Sachdeva I would like to add another diagram to the notes (I had a chance to tweak the diagram due to a question recently asked). Below are the two cases. The first is GARP's example in their Chapter 1 (which confused me for a while because the yellow 12% is broken into 10% and 2% in theirs); I think mine is a little better especially with the color although, again, the top below is essentially the same example as illustrated in GARP's chapter 1. The second is not in the notes (or source) because I just now created it, but we will add on revision.

In terms of literal (textual) examples, I think you have a good suggestion.

• In regard to unconditional dependence + conditional independence, there are many examples as this is classic idea in filtering (eg. time series) and Bayesian analysis (ie. so often we do want to "condition" out noise to achieve i.i.d.) , but I rather like the super intuitive example here at https://towardsdatascience.com/cond...the-backbone-of-bayesian-networks-85710f1b35b ; i.e., the height and vocabulary of a child is unconditionally dependent, but if you conditional on age, they are conditionally independent
• In regard to unconditional independence + conditional dependence, I'm thinking extreme stress! So i just took the second graph above, and rejiggered the numbers to product the graph below. Imagine the P(A) = 20% and P(B) = 20% and these are the (admittedly high) unconditional default probabilities. Event C (red rectangle) is macroeconomic stress and conditional on this event the default probabilities shift to dependence. I think my numbers align with the concept: unconditional independence is true because P(A)*P(B) = 20%*20% = P(A∩B) = 4.0%. However, conditionally P(A|C)*P(B|C) = 50%*50% = 25.0% ≠ P(A∩B|C) = 3.0%/8% = 37.5%. That's just to numerically align with the more intuitive idea: two bonds might be unconditionally independent with respect to default probability, but "spike" to dependence in macroeconomic stress. I hope that's useful, I'll think on better ideas but look forward to adding the illustrations to next revision of the notes.

Note: This has been added to the published Study Notes

 

[Raj Sachdeva]

@David Harper CFA FRM excellent examples David. Very helpful. The concept is now easier to grasp. Thanks!

 

[RChow4139]

I cannot understand the diagram. From where do we get the 20 percent unconditional probability and 50 percent conditional probability numbers used in the equation. Is it assumed or is it derived from the diagram ?

 

[gsarm1987]

@RChow4139 see the diagram at bottom A = 15+1+3+1 =20, B = 15+1+3+1 = 20. Re: 50%. P(A|C) = P(A&C)/P(C) = (3%+1%)/(3%+1%+1%+3%)=50%. P(B|C) = P(B&C)/P(C) = (1%+3%)/(3%+1%+1%+3%) =50%. Hint: pay attention to the rectangles