PFE of CDS and Cross Currency SWAP
- Thread starter NNath
- Start date
Hi @NNath I don't yet have a copy of the 2016 practice questions; I will look at this when I get a copy. Thanks!
Hi @David Harper CFA FRM, I just downloaded the GARP'S frm part 2 practice exam, this year I can see something is changed, there are 80 questions in this set. What's your opinion about it? And I think from many year you are also expecting form GARP to publish full exam set. Please share your thoughts.
Thank you
Thank you
@Deepak Chitnis I just received my copy. Yes, I agree, everybody preferred, for years, to see a full-length practice exam, and these are (P2 is only 80 questions, while P1 is 100 questions, I assume you realize), so that's really nice to see GARP providing full length practice exams, yay! I don't have any thoughts about the content, I haven't worked them yet myself, I just asked for a copy in order to answer @NNath Thanks!
Last edited:
@NNath
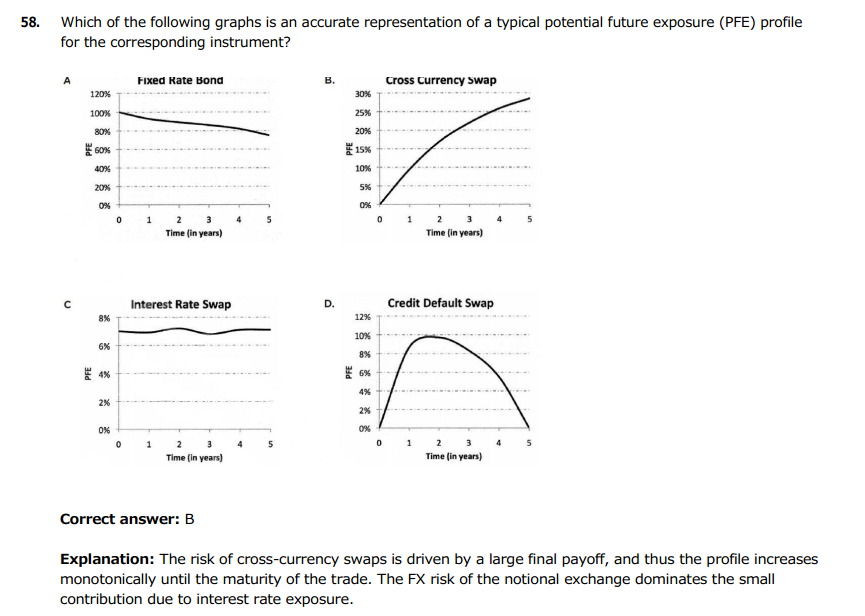
Great observation! I agree with you: using Gregory's XLS (https://www.dropbox.com/s/ym1fspf9k996b1l/Chapter8.xlsm?dl=0 ) I can generate a CDS PFE CE profile very much similar to 58(D). Below are two curves copied from my own PQ. The CDS is interesting because at each time step, the first issue is: does the default probability exceed the PDF significance? If yes, the PFE plots horizontally at LGD (1 - recovery). eg, if the PFE is 99.0% confidence, for any PD > 1%, the curve "jumps" to flat (1-recovery)! Like in mine below, the 98% PFE is plotting a 30% recovery, while the 95% PFE never breaches the PD. So, I agree with you: 58(D) appears to be a valid plot of a CDS where (100% - confidence level) never exceeds the interval's default probability. I will forward to GARP but I think an "innovative" (instructive) fix would be to label the CDS as a 99.0% profile referencing a risky credit; e.g., 99% PFE of CDS referencing obligor with 3% because then the absence of a "jump to recovery" is missing. Thanks!
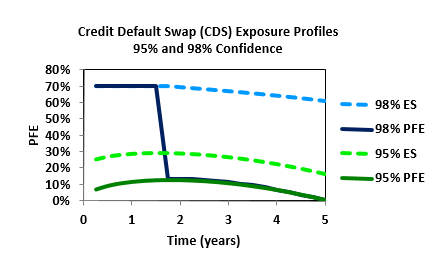
append: actually, Gregory's text (the source reading) has a straightforward example, the PFE at 95%, which supports your point:
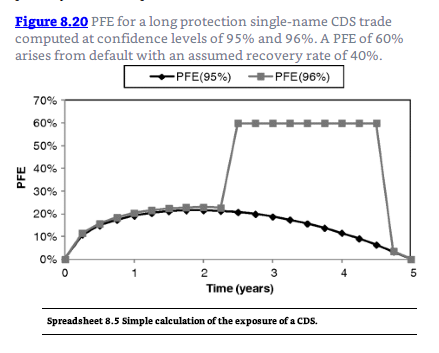
Great observation! I agree with you: using Gregory's XLS (https://www.dropbox.com/s/ym1fspf9k996b1l/Chapter8.xlsm?dl=0 ) I can generate a CDS PFE CE profile very much similar to 58(D). Below are two curves copied from my own PQ. The CDS is interesting because at each time step, the first issue is: does the default probability exceed the PDF significance? If yes, the PFE plots horizontally at LGD (1 - recovery). eg, if the PFE is 99.0% confidence, for any PD > 1%, the curve "jumps" to flat (1-recovery)! Like in mine below, the 98% PFE is plotting a 30% recovery, while the 95% PFE never breaches the PD. So, I agree with you: 58(D) appears to be a valid plot of a CDS where (100% - confidence level) never exceeds the interval's default probability. I will forward to GARP but I think an "innovative" (instructive) fix would be to label the CDS as a 99.0% profile referencing a risky credit; e.g., 99% PFE of CDS referencing obligor with 3% because then the absence of a "jump to recovery" is missing. Thanks!
append: actually, Gregory's text (the source reading) has a straightforward example, the PFE at 95%, which supports your point:
Last edited:
Hi @David Harper CFA FRM
The study notes say that "The overall high interest rates paid are expected to be offset by the gain on the notional exchange at the maturity of the contract, and this expected gain on exchange of notional leads to a significant exposure for the payer of the high interest rate." I don't understand why they are expecting a gain in this transaction? Aren't they just receiving back the initial currency exchange and doesn't the gain depend on what the FX rates are at the end of the transaction?
The study notes say that "The overall high interest rates paid are expected to be offset by the gain on the notional exchange at the maturity of the contract, and this expected gain on exchange of notional leads to a significant exposure for the payer of the high interest rate." I don't understand why they are expecting a gain in this transaction? Aren't they just receiving back the initial currency exchange and doesn't the gain depend on what the FX rates are at the end of the transaction?
Hi @bpdulog Yes, it is true that "Aren't they [i.e., the counterparty in a cross currency swap who is paying the higher interest rate] just receiving back the initial currency exchange and doesn't the gain depend on what the FX rates are at the end of the transaction?" but there is always the premise that at initiation the swap is a fair deal with initial market value of zero to both counterparties. If you are the counterparty paying the higher coupon, then the only way the swap is fair to you is if you expect the notional exchange to "make you whole." (or put another way, if the initial value is zero but you are negative cash flow in the early periods, then you must be positive in later periods). So the coupons and notional amounts are assumed to be sized to reflect the current forward rate (as a predictor of the notional value exchanged at the end of the swap). I hope that clarifies!
Last edited:
This is quite an interesting point. After covering the topic about Covered Interest Parity Lost, I recalled that Cross-currency basis swaps actually exchange notionals (at maturity) based on the initial spot rate (and not the prevailing spot rate at maturity).
So if one is paying the higher interest rate, one expects that currency to depreciate (based on covered interest parity). At maturity, if one were to swap the notionals at the spot rate prevailing at maturity, I would understand that you would make a gain (and hence have a positive exposure). However, since the notionals are swapped at the original spot rate (the FX rate at the start of the contract), there would be no gain here (perhaps even a loss!). However, the textbook disagrees at this point. I assume they are correct, however, I just can't see it yet.
Similar threads
