Questions:
611.1. Peter the portfolio manages observes the following three well-diversified portfolios (A, B and C) that exist in a single-factor economy:
.jpg)
If Peter seeks to conduct an arbitrage with a long/short portfolio with $2.0 million of gross exposure, what is the expected profit (assuming no transaction costs and no margin)?
a. No profit, as an arbitrage is not possible
b. $10,000
c. $25,000
d. $30,000
611.2. Assume security returns are generated by the single-index model: R(i) = α(i) + β(i)*R(M) + e(i); where R(i) is the excess return for security(i) and R(M) is the market's excess return. The risk free-rate is 2.0% and the volatility of the market index is 20.0%. Suppose that there are three securities, (A), (B) and (C), characterized by the following data:
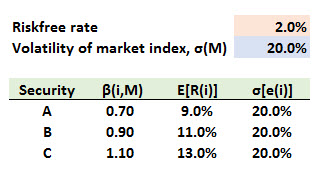
Consider the following two statements:
I. Given their identical Treynor measures, there is no arbitrage opportunity among the three securities
II. Given their identical non-systematic risk, σ[e(i]], all three securities have an identical expected (ex ante) Sharpe ratio
Which of the above statements is (are) TRUE?
a. Both statements are true
b. I. is true (there is no arbitrage opportunity); but II. is false (their Sharpe ratios differ)
c. I. is false ((there is an arbitrage opportunity) , but II. is true (their Sharpe ratios are identical)
d. Both statements are false
611.3. According to Bodie, Kane, Marcus, each of the following statements is true about arbitrage pricing theory (APT) EXCEPT which is false? (Source: Zvi Bodie, Alex Kane, and Alan J. Marcus, Investments, 10th Edition (New York: McGraw-Hill, 2013))
a. Price relationships that satisfy the no-arbitrage condition are important because we do expect them to hold in real-world markets
b. In a well-diversified portfolio, the proportion held of any individual security is small enough that a reasonable change in that security's rate of return will have a negligible effect on the portfolio's rate of return
c. The arbitrage pricing theory (APT) model is inferior to the capital asset pricing model (CAPM) because APT cannot predict a security market line linking expected return to risk due to the reality that idiosyncratic risk is not diversified away in the APT
d. The arbitrage pricing theory (APT) does not require the restrictive assumptions of the capital asset pricing model (CAPM) and its unobservable market portfolio, but the price of this generality is that the APT does not guarantee this relationship for all securities at all times.
Answers here:
611.1. Peter the portfolio manages observes the following three well-diversified portfolios (A, B and C) that exist in a single-factor economy:
.jpg)
If Peter seeks to conduct an arbitrage with a long/short portfolio with $2.0 million of gross exposure, what is the expected profit (assuming no transaction costs and no margin)?
a. No profit, as an arbitrage is not possible
b. $10,000
c. $25,000
d. $30,000
611.2. Assume security returns are generated by the single-index model: R(i) = α(i) + β(i)*R(M) + e(i); where R(i) is the excess return for security(i) and R(M) is the market's excess return. The risk free-rate is 2.0% and the volatility of the market index is 20.0%. Suppose that there are three securities, (A), (B) and (C), characterized by the following data:

Consider the following two statements:
I. Given their identical Treynor measures, there is no arbitrage opportunity among the three securities
II. Given their identical non-systematic risk, σ[e(i]], all three securities have an identical expected (ex ante) Sharpe ratio
Which of the above statements is (are) TRUE?
a. Both statements are true
b. I. is true (there is no arbitrage opportunity); but II. is false (their Sharpe ratios differ)
c. I. is false ((there is an arbitrage opportunity) , but II. is true (their Sharpe ratios are identical)
d. Both statements are false
611.3. According to Bodie, Kane, Marcus, each of the following statements is true about arbitrage pricing theory (APT) EXCEPT which is false? (Source: Zvi Bodie, Alex Kane, and Alan J. Marcus, Investments, 10th Edition (New York: McGraw-Hill, 2013))
a. Price relationships that satisfy the no-arbitrage condition are important because we do expect them to hold in real-world markets
b. In a well-diversified portfolio, the proportion held of any individual security is small enough that a reasonable change in that security's rate of return will have a negligible effect on the portfolio's rate of return
c. The arbitrage pricing theory (APT) model is inferior to the capital asset pricing model (CAPM) because APT cannot predict a security market line linking expected return to risk due to the reality that idiosyncratic risk is not diversified away in the APT
d. The arbitrage pricing theory (APT) does not require the restrictive assumptions of the capital asset pricing model (CAPM) and its unobservable market portfolio, but the price of this generality is that the APT does not guarantee this relationship for all securities at all times.
Answers here:
Last edited:

