Sixcarbs
Active Member
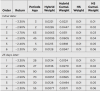
I am trying to interpolate the VaR using the hybrid method. Below is Table 1-3 from Allen.
For the initial, (top half), for 5% I interpolate between .0447 and .0511 and -2.90% and -2.70%. I get 2.73%.
.0500 is roughly 17% less than .0511 so 17% of the difference is roughly .03% which gives me the answer 2.73%.
For the bottom half I interpolate between .0494 and .0571 and -2.4% and -2.3%. I get 2.39%.
But the text inserts a third entry for each and gets a different answer for the latter.
The text inserts a return and cumulative weight half way between the two returns, -2.8%/.0479 for the first and -2.35%/.0533 for the latter. It then uses the same interpolation methods I used but comes up with a different answer for the latter.
Why must we create a false entry to interpolate the returns to a cumulative weight of .0500? Shouldn't my method work?
On a related note, I am having trouble generating the weights in excel using the formula in the text.
Trying to set up Excel table with K column and hybrid weight column.
Text says [(1-La)/(1-La^K)]*[La^(K-1)]
I thought K was the entry. Maybe it is just the total number of entries??? I think the second term (Bold) may not be Lamda to the (K-1) power but instead Lamda of the previous K.
Thanks
For the initial, (top half), for 5% I interpolate between .0447 and .0511 and -2.90% and -2.70%. I get 2.73%.
.0500 is roughly 17% less than .0511 so 17% of the difference is roughly .03% which gives me the answer 2.73%.
For the bottom half I interpolate between .0494 and .0571 and -2.4% and -2.3%. I get 2.39%.
But the text inserts a third entry for each and gets a different answer for the latter.
The text inserts a return and cumulative weight half way between the two returns, -2.8%/.0479 for the first and -2.35%/.0533 for the latter. It then uses the same interpolation methods I used but comes up with a different answer for the latter.
Why must we create a false entry to interpolate the returns to a cumulative weight of .0500? Shouldn't my method work?
On a related note, I am having trouble generating the weights in excel using the formula in the text.
Trying to set up Excel table with K column and hybrid weight column.
Text says [(1-La)/(1-La^K)]*[La^(K-1)]
I thought K was the entry. Maybe it is just the total number of entries??? I think the second term (Bold) may not be Lamda to the (K-1) power but instead Lamda of the previous K.
Thanks



