You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Calculating revised VaR Hybrid approach
- Thread starter desh
- Start date
@desh The "hybrid" approach (aka, age-weighted historical simulation) uses the cumulative weights on the furthest right column, where 0.050 is somewhere between returns of -3.60% and -3.40%. I put them in the same sheet that I was revising for a similar question elsewhere, if you want to look at http://trtl.bz/0915-hybrid-var-xls
This is really just a special case of the simple historical simulation that you are maybe thinking about, except in simple HS each return carries a weight of 1/n.
Btw, the interpolation shown in your example is not exactly the same as Linda Allen's. The interpolation above makes the mistake of interpolating twice which, in the linear interpolation is unnecessary because you get the same result. See below. The (technical) mass-centered approach is to assume that the return observation of -3.40% is a random event with 50% of its weight to the left/right. Consequently, -3.40% is centered on cumulative weight of 4.13% + 1.06%/2 = 4.66%; and -3.30% aligns with cumulative weight of 5.19%. Then interpolation from those two points leads to 3.335%. But that's very technical. Thanks,
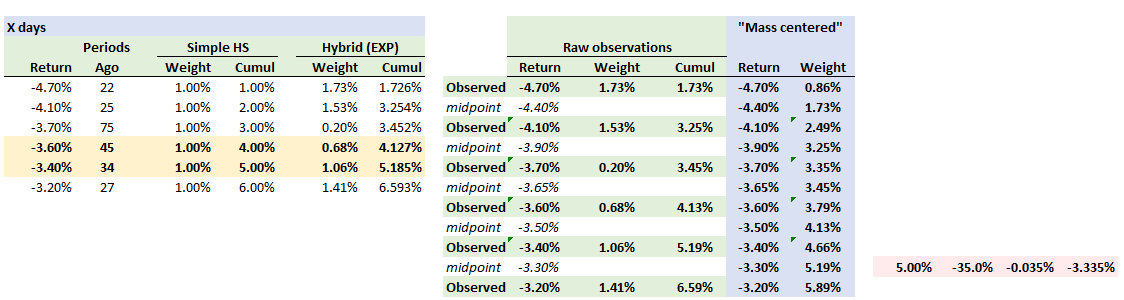
This is really just a special case of the simple historical simulation that you are maybe thinking about, except in simple HS each return carries a weight of 1/n.
Btw, the interpolation shown in your example is not exactly the same as Linda Allen's. The interpolation above makes the mistake of interpolating twice which, in the linear interpolation is unnecessary because you get the same result. See below. The (technical) mass-centered approach is to assume that the return observation of -3.40% is a random event with 50% of its weight to the left/right. Consequently, -3.40% is centered on cumulative weight of 4.13% + 1.06%/2 = 4.66%; and -3.30% aligns with cumulative weight of 5.19%. Then interpolation from those two points leads to 3.335%. But that's very technical. Thanks,

Last edited:
Hesham_87
Member
Dear David,
would you please explain the logic/concept behind VaR calculation, that is mentioned in Desh's snap shot above.
3.5%-(3.5%-3.4%)[(0.05-.0466)/(.0519-.0466)]
would you please explain the logic/concept behind VaR calculation, that is mentioned in Desh's snap shot above.
3.5%-(3.5%-3.4%)[(0.05-.0466)/(.0519-.0466)]
emilioalzamora1
Well-Known Member
This is the interpolation formula (mainly used for such simplified exercises) to determine the 95% VaR.
How is it done?
1. As a first step the weights for return at t:zero, t:1 etc. are determined. E.g., the weight for the worst loss is determined by (1-lambda)*lambda^0; for the second worst loss the formula is (1-lambda)*lambda^1 and so forth.
2. Then you sum up the weights step by step (adding the weight at t:zero to the weight at t:1, then adding the weight at t:2 to the cumulative weight from (t:0 + t:1).
3. Once you have passed the 5% mark for the cumulative weight you took the correspodning return at this point and the previous return for the interpolation. In other words, the hybrid cumulative weight of 0.0519 is your reference to watch out for. It's corresponding return is -3.4%. The other hybrid cumulative weight needed for the interpolation is 0.0413 with it's corresponding return of -3.6%.
How is it done?
1. As a first step the weights for return at t:zero, t:1 etc. are determined. E.g., the weight for the worst loss is determined by (1-lambda)*lambda^0; for the second worst loss the formula is (1-lambda)*lambda^1 and so forth.
2. Then you sum up the weights step by step (adding the weight at t:zero to the weight at t:1, then adding the weight at t:2 to the cumulative weight from (t:0 + t:1).
3. Once you have passed the 5% mark for the cumulative weight you took the correspodning return at this point and the previous return for the interpolation. In other words, the hybrid cumulative weight of 0.0519 is your reference to watch out for. It's corresponding return is -3.4%. The other hybrid cumulative weight needed for the interpolation is 0.0413 with it's corresponding return of -3.6%.
Last edited:
emilioalzamora1
Well-Known Member
Hi @David Harper CFA FRM,
I would like to reopen this discussion as there a few things unclear here which already puzzled me at the beginning of July when commenting on it.
1. Option
The 5th percentile (having n=100 datapoints) using the location formula of the percentile: (n+1)*(Y/100) >>> (100+1)*(5/100) = 5,05
As 5,05 is not an even number we would have to interpolate between the 5th and 6th worst return which would then yield (using the simple linear interpolation formula used in Choudhry):
-3.4% + { (5,05 - 5) / (6-5) * [-3.2% - (-3.4%) ] }= 3.39% This would imply that the 95% VaR is 3.39% which is different to the example (from Schweser) above.
2. Option
If we want the 95% VaR we notice that it has to lie between the cum. hybrid weight 0.0413 and 0.0519. Hence, we interpolate between the returns -3.6% and -3.4%.
Using Choudhry's interpolation formul again we have:
-3.6% + { (5% - 4.13%) / (5.19% - 4.13%) * [-3.4% - (-3.6%) ] } = 3.436% which apparently yields the same result as above (Schweser example) but I don't quite understand where the difference in results is coming from. In other words, what's differenc between 1. Option and 2. Option explained in technical terms?
And what is more important, which Option from above is more precise in nature to determine the 95% VaR?
I would like to reopen this discussion as there a few things unclear here which already puzzled me at the beginning of July when commenting on it.
1. Option
The 5th percentile (having n=100 datapoints) using the location formula of the percentile: (n+1)*(Y/100) >>> (100+1)*(5/100) = 5,05
As 5,05 is not an even number we would have to interpolate between the 5th and 6th worst return which would then yield (using the simple linear interpolation formula used in Choudhry):
-3.4% + { (5,05 - 5) / (6-5) * [-3.2% - (-3.4%) ] }= 3.39% This would imply that the 95% VaR is 3.39% which is different to the example (from Schweser) above.
2. Option
If we want the 95% VaR we notice that it has to lie between the cum. hybrid weight 0.0413 and 0.0519. Hence, we interpolate between the returns -3.6% and -3.4%.
Using Choudhry's interpolation formul again we have:
-3.6% + { (5% - 4.13%) / (5.19% - 4.13%) * [-3.4% - (-3.6%) ] } = 3.436% which apparently yields the same result as above (Schweser example) but I don't quite understand where the difference in results is coming from. In other words, what's differenc between 1. Option and 2. Option explained in technical terms?
And what is more important, which Option from above is more precise in nature to determine the 95% VaR?
Last edited:
Hi there @emilioalzamora1 !
I am honored to talk to you, I have seen the amazing clarity of the responses given by you in the forums.
If I am not wrong, you are asking why the difference arises between the two methods, right?
I would like to hazard a guess here based on my understanding of the situation (it may be wrong also)
In Option 1, you are finding out the position of the 5th worst loss by computing the position of the percentile, the location of the percentile is based on
(n+1)*percentile to find out the number of data lying under it, here, in your case, it is 5.05. There are different variations of the same rule, we can either use the formula above which I think incorporates the effect of an additional degree of freedom. Or, as I have posted in the attached Excel sheet, we can also take the 95% value of the number of the 6 worst losses, which we get as 5.7
The difference between both the above approaches is that the former method weighs the location in favor of the simple average HS location of 5th worst loss itself while the latter weighs it in favor of the 6th worst loss, i.e., asks us to find or shift the value closer to the 6th position. This approach can be seen to be applied in some companies.
A twist to the above story is that, a more acceptable approach would be to take the 6th worst loss of -3.20% as the 5 observations are assumed to be included in the tail.
Linda Allen's approach is to assign a curve based weight to the observations as opposed to the linear or simple weights that is implicitly assumed in the formulae above. We can see that the location of the values for the 5% percentile varies if we use the approach given by Linda Allen. The weight used by her, which is [(1-Lambda)*Lambda^(days-1)]/(1-Lambda^K) weights the most recent observations (the recent memory ) with a higher weight and those in the distant past to be having a smaller weight (or memory) and hence the day structure of the losses causes the 5th percentile to shift towards the -3.6% and -3.4%
As far as your final question goes, we can see that considering the minor difference in the percentage losses among the different methods, it doesn't really matter in practice which method is adopted. Although, David's approach incorporating the central mass position of the observation is the most theoretically sound and Linda's approach is the second best, companies would always like to keep it short and simple in the interests of practical difficulties encountered in implementation and operation.
Therefore, Many companies use Option 1 or the variation of it that I pointed out or even the simple Average HS, it just varies based on the Risk policy of the company to weight it to the closer (higher) of the two worst losses or the farther observation. In many cases, just take the 5th or the 6th observation as we cannot be too nitty-picky or precise as to an uncertain number- a best estimate works in 90% of the cases!
Hope this helped and I think @David Harper CFA FRM can give greater clarity here
Thanks
I am honored to talk to you, I have seen the amazing clarity of the responses given by you in the forums.

If I am not wrong, you are asking why the difference arises between the two methods, right?
I would like to hazard a guess here based on my understanding of the situation (it may be wrong also)
In Option 1, you are finding out the position of the 5th worst loss by computing the position of the percentile, the location of the percentile is based on
(n+1)*percentile to find out the number of data lying under it, here, in your case, it is 5.05. There are different variations of the same rule, we can either use the formula above which I think incorporates the effect of an additional degree of freedom. Or, as I have posted in the attached Excel sheet, we can also take the 95% value of the number of the 6 worst losses, which we get as 5.7
The difference between both the above approaches is that the former method weighs the location in favor of the simple average HS location of 5th worst loss itself while the latter weighs it in favor of the 6th worst loss, i.e., asks us to find or shift the value closer to the 6th position. This approach can be seen to be applied in some companies.
A twist to the above story is that, a more acceptable approach would be to take the 6th worst loss of -3.20% as the 5 observations are assumed to be included in the tail.
Linda Allen's approach is to assign a curve based weight to the observations as opposed to the linear or simple weights that is implicitly assumed in the formulae above. We can see that the location of the values for the 5% percentile varies if we use the approach given by Linda Allen. The weight used by her, which is [(1-Lambda)*Lambda^(days-1)]/(1-Lambda^K) weights the most recent observations (the recent memory ) with a higher weight and those in the distant past to be having a smaller weight (or memory) and hence the day structure of the losses causes the 5th percentile to shift towards the -3.6% and -3.4%
As far as your final question goes, we can see that considering the minor difference in the percentage losses among the different methods, it doesn't really matter in practice which method is adopted. Although, David's approach incorporating the central mass position of the observation is the most theoretically sound and Linda's approach is the second best, companies would always like to keep it short and simple in the interests of practical difficulties encountered in implementation and operation.
Therefore, Many companies use Option 1 or the variation of it that I pointed out or even the simple Average HS, it just varies based on the Risk policy of the company to weight it to the closer (higher) of the two worst losses or the farther observation. In many cases, just take the 5th or the 6th observation as we cannot be too nitty-picky or precise as to an uncertain number- a best estimate works in 90% of the cases!

Hope this helped and I think @David Harper CFA FRM can give greater clarity here
Thanks
emilioalzamora1
Well-Known Member
Hi @QuantMan2318
thanks for your input. Need some time to think about it but at first glance it seems a plausible explanation.
thanks for your input. Need some time to think about it but at first glance it seems a plausible explanation.
Hi @emilioalzamora1 and @QuantMan2318 I updated the previous XLS above (a copy here at http://trtl.bz/0915-hybrid-var-xls) with the calculations displayed below. Here is my perspective:

- Desh's (Schweser) example is effectively the same as @emilioalzamora1 's Option #2, which is the most straightforward (plain) linear interpolation. That's where we observe return [@ weight = 4.13%] = -3.60% and return[@ weight = 5.19%] = -3.40%. This is most intuitive because we seek 5.0% which is 82% (0.82) of the weight interval between [4.13%, 5.19%] so we also want to add 82% of the return interval between [-3.60%, -3.40] exactly as he shows above.
- The only difference with the Schweser example is that an additional, unnecessary step is taken; they linearly interpolate twice, but because it's linear, it must reach the same result(see "Desh's example below"). The first interpolation simply creates an additional pair: return[@ 4.66%] = -3.50% Then the second interpolation uses this 4.66% weight (instead of observed 4.13%) as the nearby point. I suspect the reason this was done was to try an replicate Linda Allen's method ....
- But Linda Allen's method does not interpolate twice. As shown under the "Mass centered" columns, she (and Hull actually did this too, in a previously assigned FRM reading) assumes that each return observation is a random event with 50% of its weight to its left/right. For example, under this approach, the cumulative weight of 4.127% (0.0413) does not correspond as it would seem to a return of -3.60% but rather, because it is centered on -3.60%, it extends to the midpoint of -3.60% and -3.40%, so that weight of 4.127% corresponds to return -3.50%. Then the (next) return of -3.40% includes only half of its weight (because the weight is centered here!) so that -3.40% corresponds to weight of 4.127% + 1.06%/2 = 4.66%. Once this adjustment is done, the linear interpolation is exactly the same (but with different points of course) to get the 03.335%. In this way, although there are many ways to interpolate, we so far are always just interpolating linearly. The question is whether to use the data "as is" or treat it with the more sophisticated "mass centering."
- Under Dowd's age-weighted HS (which is the same as hybrid), he seems to suggest we should do this basic linear interpolation: "For example, if we are using a spreadsheet, we can order our P/L observations in one column, put their weights w(i) in the next column, and go down that column until we reach our desired percentile. Our VaR is then the negative of the corresponding value in the first column. And if our desired percentile falls between two percentiles, we can take our VaR to be the (negative of the) interpolated value of the corresponding first-column observations." ... although he is sophisticated enough to know there are many non-linear variations... I hope that's helpful!

Last edited:
emilioalzamora1
Well-Known Member
The master brings the big guns in! Outstanding piece, @David Harper CFA FRM!
Thanks for the clarification.
Thanks for the clarification.
I just wanted to close the loop (because I was answering a similar question here at https://forum.bionicturtle.com/threads/hybrid-approach-to-compute-var.4384) in case there is a want for future reference. Shown below, on the left side panels, are Linda Allens assumptions given (in 2.2.7 The hybrid approach) under both the initial date and 25 days later. It is my opinion that she has a mistake in the text. When she computes 2.73% for the 95% hybrid VaR (initial state) she is mistakenly interpolating twice (Schweser's example is above is presumably based on this). These are shown in purple. But it's not consistent with her description of "mass centering" before interpolating, which is shown on the right panel and (according to my calculations) would produce 2.63% (instead of 2.73%). Details after the exhibit, but my evidenced includes the fact that her 25 days later 95% VaR calculates to 2.34% by correctly applying the "mass centering" methodology (but if we were to repeat the naive interpolation/2x interpolation, then we would get 2.39% instead).

Specifically, in my opinion,on page 58 instead of:
the text should read (my changes emphasized to match above exhibit):

Specifically, in my opinion,on page 58 instead of:
In contrast, the hybrid approach departs from the equally weighted HS approach. Examining first the initial period, table 2.3 shows that the cumulative weight of the −2.90 percent return is 4.47 percent and 5.11 percent for the −2.70 percent return. To obtain the 5 percent VaR for the initial period, we must interpolate as shown in figure 2.10. We obtain a cumulative weight of 4.79 percent for the −2.80 percent return. Thus, the 5th percentile VaR under the hybrid approach for the initial period lies somewhere between 2.70 percent and 2.80 percent. We define the required VaR level as a linearly interpolated return, where the distance to the two adjacent cumulative weights determines the return. In this case, for the initial period the 5 percent VaR under the hybrid approach is:
2.80% − (2.80% − 2.70%)*[(0.05 − 0.0479)/(0.0511 − 0.0479)]
= 2.73%.
Similarly, the hybrid approach estimate of the 5 percent VaR 25 days later can be found by interpolating between the −2.40 percent return (with a cumulative weight of 4.94 percent) and −2.35 percent (with a cumulative weight of 5.33 percent, interpolated from the values on table 2.3). Solving for the 5 percent VaR: 2.35% − (2.35% − 2.30%)*[(0.05 − 0.0494)/(0.0533− 0.0494)]
= 2.34%.
the text should read (my changes emphasized to match above exhibit):
In contrast, the hybrid approach departs from the equally weighted HS approach. Examining first the initial period, table 2.3 shows that the cumulative weight of the −2.90 percent return is 4.47 percent and 5.11 percent for the −2.70 percent return. To obtain the 5 percent VaR for the initial period, we must interpolate as shown in figure 2.10. We obtain a cumulative weight of 4.79 percent for the −2.80 percent return and 5.11% for -2.60% (which is the midpoint between -2.70% and -2.50%). Thus, the 5th percentile VaR under the hybrid approach for the initial period lies somewhere between 2.60 percent and 2.70 percent. We define the required VaR level as a linearly interpolated return, where the distance to the two adjacent cumulative weights determines the return. In this case, for the initial period the 5 percent VaR under the hybrid approach is:
2.70% − (2.70% − 2.60%)*[(0.05 − 0.0479)/(0.0511 − 0.0479)]
= 2.63%.
Similarly, the hybrid approach estimate of the 5 percent VaR 25 days later can be found by interpolating between the −2.35 percent return (with a cumulative weight of 4.94 percent) and −2.30 percent (with a cumulative weight of 5.3246 percent, interpolated from the values on table 2.3). Solving for the 5 percent VaR: 2.35% − (2.35% − 2.30%)*[(0.05 − 0.0494)/(0.0533− 0.0494)] [<--notice how this formula is correct; it's just the text that needs editing to match!]
= 2.34%.
Hi David - I have a question about what "weighting" does. In the HS case, each return in a series of say 100 days is ranked and then the 95% HS VaR is the 95th lowest number in the list. This is relatively straightforward. What I am confused about is the implementation of weights.
i) When we apply an age weight, do we multiply every return observation in the series by w(i) and then perform the ranking using the diminished values? Or is the weighting used purely for ranking purposes, after which you report the true loss amount as the VaR?
ii) Will the the VaR number be a weighted or unweighted value? If weighted, then assuming that n = 10, using an age weight means that w(10) = 0.0595 which means that a loss of -$1,000,000 only becomes a loss of -$59.5k, which doesn't seem to give a true picture of potential loss.
iii) Using a low lambda will mean that recent observations will almost completely dominate all older observations regardless of their value, which of course means that you will almost always end up with the VaR amount being a recent observation rather than an older observation. While I understand that's the point of age-weighting, doesn't this severely limit the ability to pick up older observations? What's a typical lambda value used in practice, and how does one derive that number?
Hope my questions are clear!
i) When we apply an age weight, do we multiply every return observation in the series by w(i) and then perform the ranking using the diminished values? Or is the weighting used purely for ranking purposes, after which you report the true loss amount as the VaR?
ii) Will the the VaR number be a weighted or unweighted value? If weighted, then assuming that n = 10, using an age weight means that w(10) = 0.0595 which means that a loss of -$1,000,000 only becomes a loss of -$59.5k, which doesn't seem to give a true picture of potential loss.
iii) Using a low lambda will mean that recent observations will almost completely dominate all older observations regardless of their value, which of course means that you will almost always end up with the VaR amount being a recent observation rather than an older observation. While I understand that's the point of age-weighting, doesn't this severely limit the ability to pick up older observations? What's a typical lambda value used in practice, and how does one derive that number?
Hope my questions are clear!
Hi @willyong Your questions are clear (and good!), I hope you don't mind, I rarely move posts but I moved your questions to this thread only because I think it could be very clarifying. My XLS above goes deeper into the weighting dynamics, but my XLS is a working reproduction of Linda Allen's Chapter 2 (Table 2.3) illustration of her "hybrid approach" (which is identical to Dowd's age-weighted because it is a hybrid of HS but using EWMA to weight the returns). I copied the upper left section to below, where the assumptions are 100 observations and λ = 0.98. Given this illustration, with respect to your questions:

- For the age-weighed VaR, we do not multiply returns by weights. Notice the sorted returns are -3.30%, -2.90% and -2.70%; the associated age-weights are 2.21%, 2.26% and 0.63%, as a function of their "periods ago." The simplest possible usage here is to retrieve -2.70% as the return that corresponds to (falls within the age-weighted bin) the worst 5.0% percentile. So just "looking up" and locating 2.70% as the 95.0% would be naive, but not wrong. The next simplest is to interpolate, and that is illustrated in purple. So you can we do not multiply the returns by the weights, although that's interesting because it's something we could do to retrieve a advanced, generalized version of the ES.
- Agreed, but since we aren't weighting as you suspected, I think this problem resolves? (I don't want to be dismissive of your mathematical instincts. In my view, you have a correct idea here. Take the three worst returns. We could retrieve -3.30%*2.21% + -2.90%*2.26% * -2.70*0.63% = -0.16%, but then we'd probably want to divide this by the sum of the weights to get the condition average: -0.16%/5.11% cumulative weight = -3.049%. And this is, to me, a generalized ES of the worst 5.11% tail; I guess it would be an age-weighted ES! ... this seems to me perfectly valid, although I don't think i've seen it anywhere!)
- Yes, absolutely! It basically undermines the purpose to select a lambda that is too low: for a low lambda, effectively only a handful of the recent observations are used and the rest are effectively discarded. With respect to typical lambda param, I refer you to Carol Alexander's Vol II at https://forum.bionicturtle.com/reso...ractical-financial-econometrics-volume-ii.91/ Please note her context is EMWA volatility not the EWMA-HS age-weighted ("hybrid") VaR that we are discussing but I think the arguments overlap such that a typical lambda would not be less than 0.80 or so. See below, emphasis mine, I hope this is helpful!:
II.3.8.2 Interpretation of Lambda: There are two terms on the right hand side of (II.3.33). The first term is (1 - λ)*r^2. This determines the intensity of reaction of volatility to market events: the smaller is λ the more the volatility reacts to the market information in yesterday’s return. The second term is λ*σ^2. This determines the persistence in volatility: irrespective of what happens in the market, if volatility was high yesterday it will be still be high today. The closer λ is to 1, the more persistent is volatility following a market shock.
Thus a high λ gives little reaction to actual market events but great persistence in volatility; and a low λ gives highly reactive volatilities that quickly die away. An unfortunate restriction of EWMA models is they assume that the reaction and persistence parameters are not independent; the strength of reaction to market events is determined by 1 − λ and the persistence of shocks is determined by λ. But this assumption is, in general, not empirically justified.
The effect of using a different value of λ in EWMA volatility forecasts can be quite substantial. For instance, Figure II.3.6 compares two EWMA volatility estimates/forecasts of the S&P 500 index, with λ = 0.90 and λ = 0.96. We can see from the figure that there are several instances when the two EWMA estimates differ by as much as 5 percentage points.
So which is the best value to use for the smoothing constant? How should we choose λ? This is not an easy question. Statistical methods may be considered: for example, λ could be chosen to minimize the root mean square error between the EWMA estimate of variance and the squared return. But more often λ is often chosen subjectively. This is because the same value of λ has to be used for all elements in a EWMA covariance matrix, otherwise the matrix is not guaranteed to be positive semi-definite. If the value of lambda is chosen subjectively the values usually range between about 0.75 (volatility is highly reactive but has little persistence) and 0.98 (volatility is very persistent but not highly reactive)."

Similar threads
- Replies
- 0
- Views
- 380
- Replies
- 0
- Views
- 143
- Replies
- 0
- Views
- 428
- Replies
- 0
- Views
- 932

