Naveen Kanth
New Member
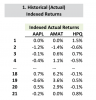
Hi in R38 P2 T5 , Reading material , page 38 in spearman's Rank correlation , example has been taken from GARP reading, it would be better if table 8.1 (In GARP reading it is completely given ) and then next step of order the return set pairs is shown . ( ranked return of X).