gargi.adhikari
Active Member
Hi,
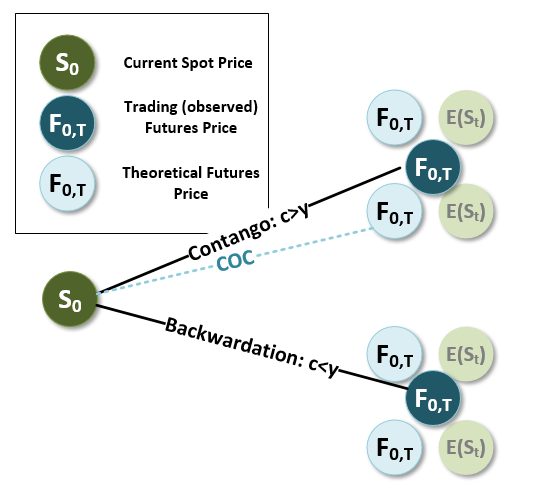
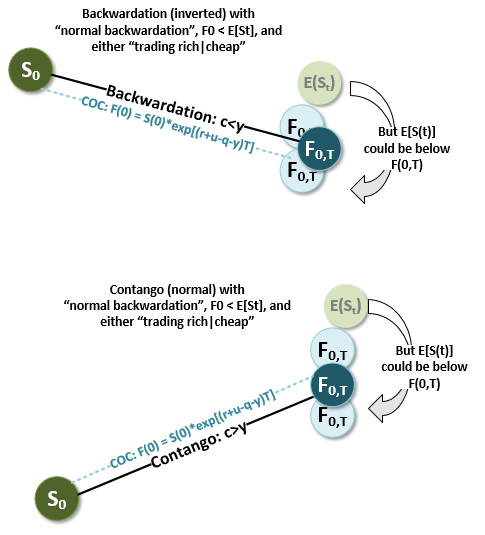
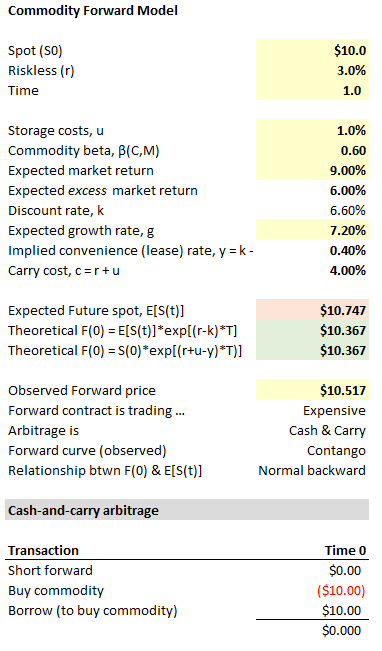
A Futures Contract is said to be Trading Rich when :
the Actual Price E(St) > the Model Predicted Price = F0=S0* EXP[ ( Rf + Storage Costs ) - ( Div + Yield ) ] T--> Normal Contango
A Short Futures Contract would Deliver as Late as possible when (Div + Yield ) > ( Rf + Storage Costs) and this happens when Futures Contract Price is decreasing with time-> Backwardation
Would it be correct to tie the "Trading Rich" condition to the "Delivery as Late as possible"
and the "Trading Cheap" condition to the "Delivery as Early as possible"
A Futures Contract is said to be Trading Rich when :
the Actual Price E(St) > the Model Predicted Price = F0=S0* EXP[ ( Rf + Storage Costs ) - ( Div + Yield ) ] T--> Normal Contango
A Short Futures Contract would Deliver as Late as possible when (Div + Yield ) > ( Rf + Storage Costs) and this happens when Futures Contract Price is decreasing with time-> Backwardation
Would it be correct to tie the "Trading Rich" condition to the "Delivery as Late as possible"
and the "Trading Cheap" condition to the "Delivery as Early as possible"