Contango, backwardation and trading cheap

[David Harper CFA FRM]

HI @flex

The second instance is simply the cost of carry model that determines a theoretical futures price based on the current spot price, S(0): Theoretical F(0) = S(0)*exp[(r+u-y)*T)]

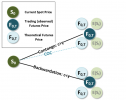
The first instance, Theoretical F(0) = E[S(t)]*exp[(r-k)*T]. relate the same theoretical futures price, F(0), to the expected future spot price, E[S(t)]. The expected future spot price, E[S(t)], is unobserved and unknown with any certainty. But my model needs to show that the theoretical futures price is the same under either approach in order to be internally coherent. Thanks,

 

[nc27]

Long time I went to visit the forum! I wanted to update one of my old post about contango/backwardation/expected future spot price/roll yield. To be honest, during a lot of time I was very confused by the theory and the possible representations (see graphics below) that a student could find on the internet.

I would like to present my views under two complementary perspectives. Let me know if you agree with me.

1) The simple cost/benefit perspective:

1.a) a future curve is in backwardation (downward sloping) if benefits (dividends + convenience yield) outweigh costs (c = risk free rate + storage costs). In short, backwardation implies b > c and Fo,T = So * exp[(c - b)*T].
1.b) a future curve is in contango (upward sloping) if costs (c = risk free rate + storage costs) outweigh benefits (b = dividends + convenience yield). In short, contango implies c > b and Fo,T = So * exp[(c - b)*T].

In a graphical representation, we would obtain an image such as the one presented by @David Harper CFA FRM,



2) The hedging perspective.

Under this perspective concepts such as expected future spot and positive/negative roll yield must be presented.

Here the difficulty, as outlined in previous posts, is to take into account an unobservable variable, the expected future spot price. To understand what this unobservable price represents we have to rely on the expectations hypothesis. Under this hypothesis we assume that the futures price will be equal to the expected spot price on the delivery date. However, the expectations hypothesis does not represent reality, since the expected future spot price is uncertain. Therefore, there must be a risk premium available to induce traders to take a position in the futures contract. The classical farmers example presented in economics textbooks allows to understand what are the main drivers of the expectations hypothesis. We present this example and how its impact our understanding of contango/backwardation/expected future spot price and roll yield.

2.a) Backwardation. Assume that some farmers want to hedge the sell price of their crops (for example corns or coffee) so they sell (short) future contracts today at lower prices than the expected delivery date spot price. This enticed the buyers of the products to enter into the long position of the contract since they can be expected to profit by the delivery date. Thus, the buyers profit = the farmers loss, but the farmers accept this in exchange for a guaranteed price for their product. Since, in this set up, the future price is below the expected future price we say that the curve is in backwardation.

2.b) Contango. Assume that the buyers of the products are the natural hedgers since they also want a guaranteed price, so they are willing to pay a higher price than the expected spot price to achieve that result. This results in higher future prices for longer-term contracts. So contango exists in a futures market when future prices increase progressively with longer maturities. This is the most common situation, since many commodities, which are traded with futures contracts, have carrying costs (such as storage costs) plus there must be some compensation for the risk of holding the underlying asset.

So under the hedging perspective, an excess of sellers (short positions) will cause a normal backwardation, whereas an excess of buyers (long positions) will result in contango. We will obtain a graphical representation such as the one presented below,


As you can observe, the contango is now downward sloping (versus upward sloping in the previous image) and the backwardation is upward sloping (versus downward sloping in the previous image). Does this mean that we have an inconsistency between the two perspectives (cost/benefit -- hedging) ? Short answer, NO!

Do not let the graphical representations fool you, the curves are the same under the two perspective and represent two complementary ideas. For example, in a contango market, the future price will increase with respect to the spot price (observable today) as maturity increases (cost/benefit perspective) and the same future price will decrease with respect to the expected future spot price (unobservable today) as maturity increases (hedging perspective). The same (reversed) idea applies for a backwardation market.

3) Positive and negative roll yield

Finally, once we understand those ideas well, we can present the idea of roll yield. In futures markets, contracts expire before their specified delivery dates. To maintain an ongoing position, futures investors need to exit contracts close to expiration and enter contracts with more distant expiration dates. This fact has given rise to the idea of a roll yield, where investors can make gains or losses when rolling from one contract to the next on the same underlying good. We now present the idea of positive and negative roll yields associated with backwardation and contango market.

In a backwardation market, the future price is lower than the expected spot price. If an investor roll a future contract in this kind of market, she will gain money. Example: An investor is interested by some corn future contracts. The spot price of corn is $100. The December future contract is $95 and the March future contract is $85.

Change in the Future’s Price = $95 – $85 = $10
Change in the Spot Price = $100 – $100 = $0
Roll Yield (positive) = Change in the Future’s Price - Change in the Spot Price = $10 – $0 = $10

In a contango market, the future price is higher than the expected spot price. If an investor roll a future contract in this kind of market, she will lose money. Example: An investor is interested by some corn future contracts. The spot price of corn is $100. The December future contract is $105 and the March future contract is $115.

Change in the Future’s Price = $105 – $115 = - $10
Change in the Spot Price = $100 – $100 = $0
Roll Yield (negative) = Change in the Future’s Price - Change in the Spot Price = - $10 – $0 = - $10

I hope this help,
Nicolas