You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
[VaR Mapping] Cash-Flow Mapping
- Thread starter silver7
- Start date
Hello @silver7Could anyone explain to me how you arrive at the 6.6234 on page 26? Thanks so much!
View attachment 1466
Can you please be specific about which set of study notes you are referring to? There are many sets of notes under the Market Risk topic. It would also be helpful to know, as we can search the forum to see if your question has already been answered in another thread.

Thank you,
Nicole
Hi @silver7
The $6.6234 is a essentially a portfolio variance (scaled/multiplied by the 1.645 deviate) in matrix form; so it's really the same 2-asset portfolio variance except generalized here to five positions, where each position is an individual VaR (the risk of a single cash flow which has been mapped to one of the five vertices; aka, risk factors). A portfolio variance is given by--to use Jorion's notation--the fundamentally important w' * Σ * w, where Σ is a covariance matrix and (w) is the vector of weights/positions, such that w' is the transposed vector. The calculation you pasted is from my replication of Jorion's Table 11-4, of course. This Table 11-4 that produces the $6.6234 is just a variation on this classic portfolio variance, is how I look at it. Just as covariance embeds correlation into the 2-asset special case--i.e., covariance(1,2) = σ(1)*ρ(1,2)*σ(2)--the portfolio variance breaks down further if we want to specify the correlation matrix (which is used as an input) rather then the covariance matrix, such that this $6.6234 = (xV')*R*(xV), where (R) is the correlation matrix, (xV) = the (column) vector of individual VaRs (e.g., $0.4917) which are themselves the produce of the PF of CF (x) and the Risk(%), and (xV') is the same but transposed in the row vector. First step is post-multiply the R*(xV), then pre-multiply (xV')*[R*(xV)] to get th $6.6234. This is all in the learning XLS, including the matrix calculations.
In regard to Jorion's Table 11-6 / 11-7 (the second exhibit):
The $6.6234 is a essentially a portfolio variance (scaled/multiplied by the 1.645 deviate) in matrix form; so it's really the same 2-asset portfolio variance except generalized here to five positions, where each position is an individual VaR (the risk of a single cash flow which has been mapped to one of the five vertices; aka, risk factors). A portfolio variance is given by--to use Jorion's notation--the fundamentally important w' * Σ * w, where Σ is a covariance matrix and (w) is the vector of weights/positions, such that w' is the transposed vector. The calculation you pasted is from my replication of Jorion's Table 11-4, of course. This Table 11-4 that produces the $6.6234 is just a variation on this classic portfolio variance, is how I look at it. Just as covariance embeds correlation into the 2-asset special case--i.e., covariance(1,2) = σ(1)*ρ(1,2)*σ(2)--the portfolio variance breaks down further if we want to specify the correlation matrix (which is used as an input) rather then the covariance matrix, such that this $6.6234 = (xV')*R*(xV), where (R) is the correlation matrix, (xV) = the (column) vector of individual VaRs (e.g., $0.4917) which are themselves the produce of the PF of CF (x) and the Risk(%), and (xV') is the same but transposed in the row vector. First step is post-multiply the R*(xV), then pre-multiply (xV')*[R*(xV)] to get th $6.6234. This is all in the learning XLS, including the matrix calculations.
In regard to Jorion's Table 11-6 / 11-7 (the second exhibit):
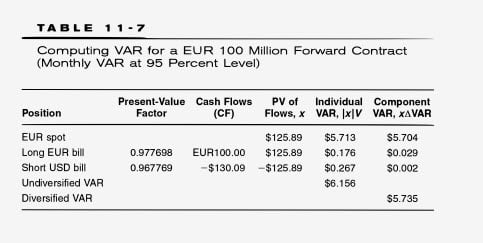
- Individual VaRs = PV of flows * VaR(%); e.g., $5.72 = 125.93 * 4.5381%; as usual, the sum of Individual VaRs = undiversified VaR (= diversified VaR if all pairwise ρs = 1.0)
- Marginal VaR = α 1.645 * cov(factor i, factor j,)/
varianceσ(portfolio) per Jorion 7.17; i.e., marginal VaR is a direct function of beta(i, P) - Component VaR = PV of flows * Marginal VaR; i.e., $5.706 = $125.93 * 0.0453
- Diversified VaR is the sum of component VaRs, as it must be
Last edited:
@David Harper CFA FRM
Thanks for the detailed explanation!
For the second exhibit, could you also explain how you arrive at the PV of the flows, $125.93.
I tried to use the 'short USD bill' rate to get it (125.93 = (100 * 1.3013) / (1 + 3.330%) ) and I cannot seem to arrive at that number from a different path. I am not sure if this is the correct way and why it is correct (why in the first two rows, it is all positive 125.93, etc)
Also, for the Marginal VaR bullet point, how do you get the variance(portfolio)?
Thanks!
Thanks for the detailed explanation!
For the second exhibit, could you also explain how you arrive at the PV of the flows, $125.93.
I tried to use the 'short USD bill' rate to get it (125.93 = (100 * 1.3013) / (1 + 3.330%) ) and I cannot seem to arrive at that number from a different path. I am not sure if this is the correct way and why it is correct (why in the first two rows, it is all positive 125.93, etc)
Also, for the Marginal VaR bullet point, how do you get the variance(portfolio)?
Thanks!
Hi @silver7 sure thing!
I got -$130.13 = -$100.00 * $1.3013 EUR forward, such that -$125.93 = -$130.13 * 0.967769 = -$130.13 * 1/(1+3.330% Short USD bill), so expanded I got it with (-$100.00 * $1.3013)* 1/(1+3.330%), so actually it looks like I took the same path you did! And the $1.303 itself is based on IRP/COC: $1.3013 = $1.2877*exp(3.330% - 2.281%), so I guess the fully expanded route is given by (-$100.00 * $1.2877*exp(3.330% - 2.281%)* 1/(1+3.330%). Jorion almost always assumes annual compounding. Mine is slightly different than Table 11-6 but, at the time, I was pretty convinced this was mere difference due to rounding; I don't think his examples take the dollar amount out far enough to be sure which IRP assumption is solving for the other, but I think my calcs comport with his description. I copied his below, where his -130.09 corresponds to my -130.13 and his -125.89 corresponds to my 125.93 that you are asking about.
And the $1.303 itself is based on IRP/COC: $1.3013 = $1.2877*exp(3.330% - 2.281%), so I guess the fully expanded route is given by (-$100.00 * $1.2877*exp(3.330% - 2.281%)* 1/(1+3.330%). Jorion almost always assumes annual compounding. Mine is slightly different than Table 11-6 but, at the time, I was pretty convinced this was mere difference due to rounding; I don't think his examples take the dollar amount out far enough to be sure which IRP assumption is solving for the other, but I think my calcs comport with his description. I copied his below, where his -130.09 corresponds to my -130.13 and his -125.89 corresponds to my 125.93 that you are asking about.
Re: Also, for the Marginal VaR bullet point, how do you get the variance(portfolio)? Sorry, my typo above, I meant standard deviation not variance so should be: Marginal VaR = α 1.645 * cov(factor i, factor j,)/σ(portfolio) per Jorion 7.17; i.e., marginal VaR is a direct function of beta(i, P). That's actually why I wrote "direct function of" rather than "equal to" beta. I hope that's helpful, when I get time later this year, I can't wait to really polish the XLS and the associated notes on this mapping section.
I got -$130.13 = -$100.00 * $1.3013 EUR forward, such that -$125.93 = -$130.13 * 0.967769 = -$130.13 * 1/(1+3.330% Short USD bill), so expanded I got it with (-$100.00 * $1.3013)* 1/(1+3.330%), so actually it looks like I took the same path you did!
 And the $1.303 itself is based on IRP/COC: $1.3013 = $1.2877*exp(3.330% - 2.281%), so I guess the fully expanded route is given by (-$100.00 * $1.2877*exp(3.330% - 2.281%)* 1/(1+3.330%). Jorion almost always assumes annual compounding. Mine is slightly different than Table 11-6 but, at the time, I was pretty convinced this was mere difference due to rounding; I don't think his examples take the dollar amount out far enough to be sure which IRP assumption is solving for the other, but I think my calcs comport with his description. I copied his below, where his -130.09 corresponds to my -130.13 and his -125.89 corresponds to my 125.93 that you are asking about.
And the $1.303 itself is based on IRP/COC: $1.3013 = $1.2877*exp(3.330% - 2.281%), so I guess the fully expanded route is given by (-$100.00 * $1.2877*exp(3.330% - 2.281%)* 1/(1+3.330%). Jorion almost always assumes annual compounding. Mine is slightly different than Table 11-6 but, at the time, I was pretty convinced this was mere difference due to rounding; I don't think his examples take the dollar amount out far enough to be sure which IRP assumption is solving for the other, but I think my calcs comport with his description. I copied his below, where his -130.09 corresponds to my -130.13 and his -125.89 corresponds to my 125.93 that you are asking about.
"This shows that the forward position can be separated into three cash flows: (1) a long spot position in EUR, worth EUR 100 million = $130.09 million in a year, or (Se-r*r) = $125.89 million now, (2) a long position in a EUR investment, also worth $125.89 million now, and (3) a short position in a USD investment, worth $130.09 million in a year, or (Ke-YZ) = $125.89 million now. Thus a position in the forward contract has three building blocks:
Long forward contract = long foreign currency spot + long foreign currency bill + short U.S. dollar bill
Considering only the spot position, the VAR is $125.89 million times the risk of 4.538 percent, which is $5.713 million. To compute the diversified VAR, we use the risk matrix from the data in Table 11-6 and pre- and postmultiply by the vector of positions (PV of flows column in the table). The total VAR for the forward contract is $5.735 million. This number is about the same size as that of the spot contract because exchange-rate volatility dominates the volatility of 1-year bonds." -- Philippe Jorion. Value at Risk, 3rd Ed.: The New Benchmark for Managing Financial Risk (p. 292). Kindle Edition.
Re: Also, for the Marginal VaR bullet point, how do you get the variance(portfolio)? Sorry, my typo above, I meant standard deviation not variance so should be: Marginal VaR = α 1.645 * cov(factor i, factor j,)/σ(portfolio) per Jorion 7.17; i.e., marginal VaR is a direct function of beta(i, P). That's actually why I wrote "direct function of" rather than "equal to" beta. I hope that's helpful, when I get time later this year, I can't wait to really polish the XLS and the associated notes on this mapping section.
Hi @silver7
The $6.6234 is a essentially a portfolio variance (scaled/multiplied by the 1.645 deviate) in matrix form; so it's really the same 2-asset portfolio variance except generalized here to five positions, where each position is an individual VaR (the risk of a single cash flow which has been mapped to one of the five vertices; aka, risk factors). A portfolio variance is given by--to use Jorion's notation--the fundamentally important w' * Σ * w, where Σ is a covariance matrix and (w) is the vector of weights/positions, such that w' is the transposed vector. The calculation you pasted is from my replication of Jorion's Table 11-4, of course. This Table 11-4 that produces the $6.6234 is just a variation on this classic portfolio variance, is how I look at it. Just as covariance embeds correlation into the 2-asset special case--i.e., covariance(1,2) = σ(1)*ρ(1,2)*σ(2)--the portfolio variance breaks down further if we want to specify the correlation matrix (which is used as an input) rather then the covariance matrix, such that this $6.6234 = (xV')*R*(xV), where (R) is the correlation matrix, (xV) = the (column) vector of individual VaRs (e.g., $0.4917) which are themselves the produce of the PF of CF (x) and the Risk(%), and (xV') is the same but transposed in the row vector. First step is post-multiply the R*(xV), then pre-multiply (xV')*[R*(xV)] to get th $6.6234. This is all in the learning XLS, including the matrix calculations.
In regard to Jorion's Table 11-6 / 11-7 (the second exhibit):
I do totally realize the notes can do a better job explaining all of this. With each iteration, we are improving the explanation. I hope this is helpful, thanks!
- Individual VaRs = PV of flows * VaR(%); e.g., $5.72 = 125.93 * 4.5381%; as usual, the sum of Individual VaRs = undiversified VaR (= diversified VaR if all pairwise ρs = 1.0)
- Marginal VaR = α 1.645 * cov(factor i, factor j,)/
varianceσ(portfolio) per Jorion 7.17; i.e., marginal VaR is a direct function of beta(i, P)- Component VaR = PV of flows * Marginal VaR; i.e., $5.706 = $125.93 * 0.0453
- Diversified VaR is the sum of component VaRs, as it must be
Hi David
I am trying to get my head around how Rxv is being calculated. Could you throw some light on that? I tried summing up the correlation (across different tenors) and then multiplying it with xv but it didnt match. Appreciate if you can help?
Thanks
Arun
Hi David
I am trying to get my head around how Rxv is being calculated. Could you throw some light on that? I tried summing up the correlation (across different tenors) and then multiplying it with xv but it didnt match. Appreciate if you can help?
Thanks
Arun
Please ignore..got the answer!
hi @David Harper CFA FRM ,
could you kindly explain why are we long eur spot as well? i get the long eur bill and short us bill (both are what you will receive and pay in the future). How does the spot comes into play? Is it meant for the conversion of the discounted EUR to USD? but whats the conversion for?
Thanks
Joe
could you kindly explain why are we long eur spot as well? i get the long eur bill and short us bill (both are what you will receive and pay in the future). How does the spot comes into play? Is it meant for the conversion of the discounted EUR to USD? but whats the conversion for?
Thanks
Joe
Hi @jtankx90 If we were VaR mapping a forward rate agreement (FRA), then we would map only to a short and long risk-free spot interest rates (i.e, short and long T-bills) as primitives. However, the above refers to a forward currency contract; aka, foreign exchange (FX) forward contract. Consequently, the current value of such a contract is highly dependent on the currency exchange rate! So, we need to map to the appropriate primitive(s), which includes the current (spot) exchange rate. As usual, we can "discover" the mapping by looking at the price function, in this case:
Per cost of carry (aka, interest rate parity in the FX contact): FX F(0) = S(0) * [exp(r - rf)*T].
So the theoretical forward current price is a function of the three primitives to which we map: the spot FX, S(0), and the two short/long risk-free rates, r and rf. I hope that explains!
Per cost of carry (aka, interest rate parity in the FX contact): FX F(0) = S(0) * [exp(r - rf)*T].
So the theoretical forward current price is a function of the three primitives to which we map: the spot FX, S(0), and the two short/long risk-free rates, r and rf. I hope that explains!
Last edited:
Rohit
Member
Hi @David Harper CFA FRM can you explain how the component VAR for FRA is calculated? My spreadsheet when mmult the correl matrix and indiv var is resulting in diff values
Hi @Rohit Please see my draft XLS here (which recreates Jorion's Table 11-7; FRA mapping): https://www.dropbox.com/s/oh5i7hdpivj5szd/jorion-11-7-fra-mapping.xlsx?dl=0
ie, component VaRs, per Jorion's label, are product of PV of CF ("x") and the Marginal VaRs, which i did successfully calculate (no time to explain all of that, see XLS). Hope this helps,

ie, component VaRs, per Jorion's label, are product of PV of CF ("x") and the Marginal VaRs, which i did successfully calculate (no time to explain all of that, see XLS). Hope this helps,

Rohit
Member
@David Harper CFA FRM thank you so much! Would the calc same apply to FRAs?
Hi @Rohit Yes! My previous illustrates the forward currency contract. To map the FRA, we can think of it as simply removing the mapping to the spot exchange rate (the currency primitive): on the XLS, I recreated by literally removing that row. Then the FRA maps only to the two spot rates (i.e., 2 primitive factors), my XLS is here (but it hasn't been polished to look good sorry): https://www.dropbox.com/s/34q016o1hvin98d/011320-jorion-11-9-FRA.xlsx?dl=0
Hi @Rohit Please see my draft XLS here (which recreates Jorion's Table 11-7; FRA mapping): https://www.dropbox.com/s/oh5i7hdpivj5szd/jorion-11-7-fra-mapping.xlsx?dl=0
ie, component VaRs, per Jorion's label, are product of PV of CF ("x") and the Marginal VaRs, which i did successfully calculate (no time to explain all of that, see XLS). Hope this helps,

Hello David I hope you are doing well.
First, I notice that the VaR Mapping calculation methods between fixed income and outright forward are different.
For fixed income we pre-and-postmultiply the correlation matrix to individual var ( CF * Z95%) and obtain a diversified VaR.
in FRA we start from correlation -> standard deviation -> covariance -> portfolio variance -> marginal. Seems to me a lot more step for FRA is required to get the answer.
Might you please provide some insight for me to further understand why they need different approaches? or perhaps they are the same and I should study a bit more of the maths behind?
[edited 5 mins after I posted this question: the video Youtube video here actually illustrated they are the same. My first question is down. Still struggling with my second question below]
Second, I notice at outright forward calculation the portfolio variance is calculated using PVCF as weight, instead of their portion in the portfolio. Might you please also elaborate why we can use actual CF to obtain the portfolio variance, rather than their corresponding weights?
Thank you!
[second edit: Seems the BSM mapping is missing from the excel downloaded from study planner R36-P2-T5-Jorion-mapping-backtest-v3.xlsx]
Last edited:
Similar threads
- Replies
- 0
- Views
- 1K
