VAR and expected loss

[hellohi]

dear @David Harper CFA FRM

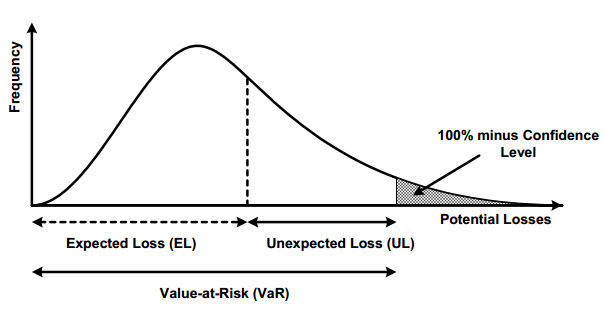
just want to ask if VAR includes expected loss? in the following chart, it seems that the VAR = EL + UL, not just unexpected loos....so this made me confused because as I knew that the expected loss is not risk, so how it be part of VAR?

best regards
Nabil

 

[ShaktiRathore]

Hi,
EL is not a risk as its already being accounted for what is risk are the losses that can happen beyond and above the expected loss therefore this losses above the EL are unpredictable are called the unexpected losses is the risky part. Thus EL+UL is a risk because the component UL is a risk(volatile UL makes the EL+UL volatile hence risky) therefore EL+UL is a risk overall thus Var=EL+UL is a risk.
thanks

 

[David Harper CFA FRM]

@hellohi see also this thread https://forum.bionicturtle.com/threads/frm-fun-13-absolute-versus-relative-var-versus-ul.6020/ (there is years of discussion on this forum, search "relative VaR" or "absolute VaR"

In super brief, where aVaR = absolute VaR and rVaR = relative VaR:

• Credit: aVaR = EL + UL, and rVaR = UL. In credit risk, VaR is ambiguous and needs to be defined because it can be defined as rVaR (e.g., Malz defines CVaR as rVaR) but can be defined as aVaR (e.g., as shown above, Basel tends to define CVaR as aVaR).
  
• Market: aVaR = -drift + UL; ie, -µ*Δt + α*σ*sqrt(t), and rVaR = UL. In market risk, best is to assume aVaR.
  
• Ops: aVaR = EL + UL, and rVaR = UL

Your diagram (which matches Basel, and looks like it might be from Basel) is showing a credit risk distribution and, by including EL, is implicitly referring to an absolute VaR: loss relative to the initial (current) position.