Valuatn & Risk Model: Hull 11,13, 17
- Thread starter skoh
- Start date
Hi skoh,
I don't think so. Where higher values are are to the right, lognormal is positively skewed (see skew at http://en.wikipedia.org/wiki/Log-normal_distribution ) and, consistent with our working definition of positive (negative) skew as long right (left) tail (2012 GARP Sample P2.question 6 is an illustration of this use of skew), the lognormal price has long right/upper tail but is capped on left/down by zero (asset price cannot go below zero). And, although positive skew does not always imply mean > median, in a lognormal this is the case (source: McDonald). Thanks,
I don't think so. Where higher values are are to the right, lognormal is positively skewed (see skew at http://en.wikipedia.org/wiki/Log-normal_distribution ) and, consistent with our working definition of positive (negative) skew as long right (left) tail (2012 GARP Sample P2.question 6 is an illustration of this use of skew), the lognormal price has long right/upper tail but is capped on left/down by zero (asset price cannot go below zero). And, although positive skew does not always imply mean > median, in a lognormal this is the case (source: McDonald). Thanks,
Hi skoh,
It's given in the answer, and it can be shown mathematically, but the idea is that, with respect to delta, dF/dS, the key difference between a futures and forward contract is the daily settlement: for the same movement in the spot price, for example $1.0 increase in the spot price, the present value of your forward gain is $1.0 because you wait for settlement, but the PV of the futures contract gain is slightly more at $1.0*exp(rT) because you settle that gain immediately.
From Answer to 17.21:
"The value of a forward contract on the asset is S0*EXP( -qT) – K*EXP(-rT). When there is a small change, ΔS, in S0 the value of the forward contract changes by EXP(-qT)* ΔS. The delta of
the forward contract is therefore EXP(-qT).
The futures price is S0*EXP((r-q)*T). When there is a small change, ΔS, in S0 the futures price change by ΔS*EXP((r-q)*T). Given the daily settlement procedures in futures contracts, this is also the immediate change in the wealth of the holder of the of the futures contract. The delta of the futures contract is therefore EXP((r-q)*T). The deltas of a futures and forward contract are not the same. The delta of the futures is greater than the delta of the corresponding forward by a factor of EXP(rT).
Please note that in regard to non-dividend-paying stock:
It's given in the answer, and it can be shown mathematically, but the idea is that, with respect to delta, dF/dS, the key difference between a futures and forward contract is the daily settlement: for the same movement in the spot price, for example $1.0 increase in the spot price, the present value of your forward gain is $1.0 because you wait for settlement, but the PV of the futures contract gain is slightly more at $1.0*exp(rT) because you settle that gain immediately.
From Answer to 17.21:
"The value of a forward contract on the asset is S0*EXP( -qT) – K*EXP(-rT). When there is a small change, ΔS, in S0 the value of the forward contract changes by EXP(-qT)* ΔS. The delta of
the forward contract is therefore EXP(-qT).
The futures price is S0*EXP((r-q)*T). When there is a small change, ΔS, in S0 the futures price change by ΔS*EXP((r-q)*T). Given the daily settlement procedures in futures contracts, this is also the immediate change in the wealth of the holder of the of the futures contract. The delta of the futures contract is therefore EXP((r-q)*T). The deltas of a futures and forward contract are not the same. The delta of the futures is greater than the delta of the corresponding forward by a factor of EXP(rT).
Please note that in regard to non-dividend-paying stock:
- Delta of forward = 1.0
- Delta of futures contract = EXP(rT)"
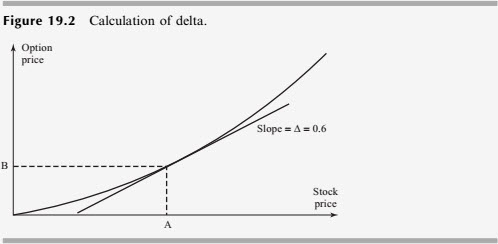
Hi @lRRAngle Forwards sort of do have a strike price (aka, delivery price). In both cases (options and forwards), the strike/delivery is a predetermined, fixed price to be paid in the future. I suppose there are a few ways to think about it; e.g., delta is a ultimate first partial derivative, the change in the derivative's value with respect to a small change in the underyling's spot price, ∂c/∂c or ∂F/∂S, so we can think mathematically. But it's maybe easier to think visually: delta is the slope of the tangent line. I'm sure you've seen the payoff diagrams: the futures payoff is linear, the options payoff is decidedly non-linear. See Hull's Figure 19.2 below. One way to think about this is that the option's payoff, and price, is bounded at zero; but the forward's price is not, it "goes negative" in a straight line (moving right to left). The slope of the option-vs-stock price tangent line, consequently, is tending to zero, as we move left; and tending to 1.0 as we move right. Visually, the difference can be seen in the behavior of this tangent, but it can be shown mathematically too. I hope that helps.
Similar threads
