Hi @David Harper CFA FRM
I am not able to understand below context. kindly help
Updated by Nicole to note that this is regarding the study notes in T2 - Chapter 10 Stationary Time Series on page 13.
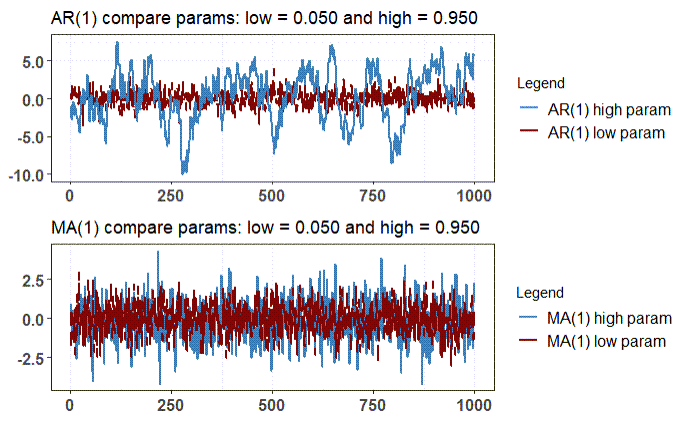
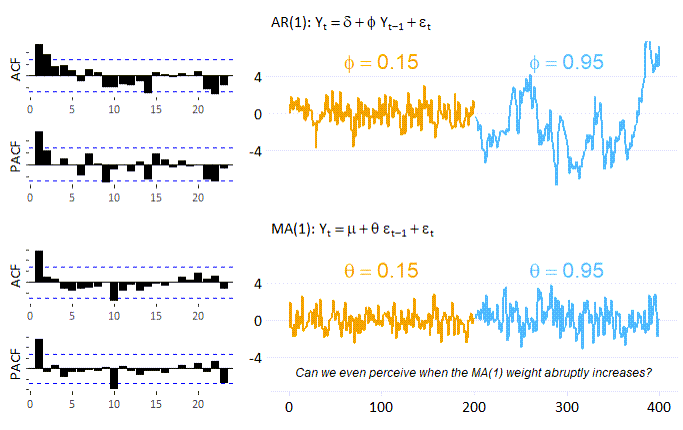
As shown in the moving average process building equation above, the lagged shocks feed positively into the current value of the series, with a coefficient value of 0.4 and 0.95 in both the cases. It would be an obvious & false assumption that θ= 0.95 would induce much more persistence than θ= 0.4. It is a false assumption because the structure of the above MA(1) process accounts only for the first lag of the shock, leading to a short-lived memory usage in process building and the value of coefficient really does not have substantial impact on the dynamics of the process.

I am not able to understand below context. kindly help
Updated by Nicole to note that this is regarding the study notes in T2 - Chapter 10 Stationary Time Series on page 13.
As shown in the moving average process building equation above, the lagged shocks feed positively into the current value of the series, with a coefficient value of 0.4 and 0.95 in both the cases. It would be an obvious & false assumption that θ= 0.95 would induce much more persistence than θ= 0.4. It is a false assumption because the structure of the above MA(1) process accounts only for the first lag of the shock, leading to a short-lived memory usage in process building and the value of coefficient really does not have substantial impact on the dynamics of the process.

Last edited by a moderator: