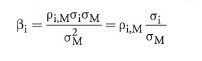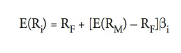YouTube T1-8 Capital market line (CML) versus security market line (SML)

[Nicole Seaman]

The CML contains ONLY efficient portfolios (and plots return against volatility; aka, total risk) while the SML plots any portfolio (and plots return against beta; aka, systematic risks) including inefficient portfolios.

The XLS David used in the video is located here https://trtl.bz/2Fru70r

 

[Eustice_Langham]

Thankyou David, its always been something of a mystery how the SML morphs into the CML, now I know. I do have a question however concerning points along the CML to the right and left of the point of tangency ie market portfolio.

In another of your videos on this point you make the comment that to the left of the market portfolio, investors are lending money at the risk free rate, but isn't this an exaggeration? I ask this because points to the immediate left of the market portfolio, there is still some risk involved in establishing your portfolio at this point, its only when you invest entirely in risk free assets eg Treasuries that your investments are risk free.

Conversely to points of the right of the market portfolio, investors are borrowing to leverage their investments, is the "gap" between the CML and the PPC, that gets wider as you take on more risk the same as the amount of leverage that an investor is taking for the additional return?

Thankyou

 

[David Harper CFA FRM]

Hi @Eustice_Langham It might help to view the XLS, here is a simple one-sheet version https://www.dropbox.com/s/q4l43w3n1le5z8h/082520-cml.xlsx?dl=0

This concerns the CML (to my knowledge, it does not require SML/CAPM; for example, Elton who was the prior author in one of the authoritative texts on MPT established the CML prior to the SML). The red dot is the Market Portfolio; it earns such stats because it has the highest Sharpe ratio on the (green) portfolio possibilities curve (PPC). On the single-sheet version I shared, the market portfolio is just a mix of two assets, but in my larger XLS, they are solved-for: they are the mix of risky assets that generates the highest Sharpe ratio (i.e., excess return divided by standard deviation). So the big step before the riskfree asset is introduced is establishing this highest-Sharpe Market portfolio. If we stay on the green PPC, moving in either direction (by definition) implies a decrease in the Sharpe ratio.

They way that I look at this (I say it that way because this is one of the most studied topics in finance, I'm sure there is a more sophisticated way to look at it given the hundreds of finance professors who've analyzed this! ....) is: the riskfree asset gives us (the investor) a way to invest at the same Sharpe ratio over a continuum of risk/reward spectrum as represented by the CML. You can see in the XLS how, if we have a Market portfolio defined, the CML is a dead simple linear function, anchored at the riskfree rate and running through the Market portfolio (aka, tangency to the PPC at the Market Portfolio). Every point on the CML has the same (optimal) Sharpe ratio as the Market portfolio. Moving up/down is not re-mixing risky assets, it is remixing between only two assets: the riskfree rate and the market portfolio. Going "up the CML" is mixing less risk free (by borrowing) and more of the Market Portfolio; going "down the CML" is mixing more riskfree (by lending; aka, investing) and less of the Market Portfolio.

You can see in the XLS how movement up/down the CML is simply shifting the weights:
E(return) = (%_riskfree) * Rf + (1 - %_riskfree)*E(return_market_portfolio).

The associated standard deviation, per basic variance properties, is simply (1 - %_riskfree)*σ(M) ... because the riskfree asset has no volatility.

If we (as the investor) choose the market portfolio, our CML decision is: 100% market portfolio plus 0% riskfree rate.
If we want less risk, we can "move down the CML" and decide: 50% market portfolio plus 50% riskfree rate. Our expected return and volatility will reduce, but our 50/50 decision will have the same Sharpe ratio (by even visual definition).

So, I think that's what I meant by investing at the riskfree rate: after the Rf has been introduced, the efficient frontier is the CML. Visually, we can see that every point on the (green) PPC, except the Market portfolio, is less efficient than any point on the (blue) CML. Consequently, our best choice is along the CML. And the CML is a mix between x% invested at the riskfree rate (or borrowed at riskfree rate) plus (1 - x%) invested in the same Market Portfolio as the other investors. The CML represents an asset allocation decision between two assets, the riskfree asset and the Market Portfolio (itself already optimal among risky assets).

Hence the way I look at it: the CML (via the Rf assets) "transforms" a single point (Market Portfolio) into a line which avails us of the same efficiency (highest Sharpe!) but at various, desired levels of risk/reward.

I hope that's helpful!

 

[Eustice_Langham]

Thanks David, my initial understanding of the SML morphing into the CML was therefore incorrect, thankyou for clearing it up.

 

[Amierul]

Hi David, I have a question here. SML Beta formula is

With regards to CAPM SML formula it is given as


But why the line is not a curve when the correlation is less than 1?

 

[David Harper CFA FRM]

Hi @Amierul Because the SML is effectively a straight line in the slope-intercept form, y = mx + b where the constant slope is the market's excess return, E(Rm) - Rf, and the X-axis is beta, β. So just to map to this more-familiar y = mx + b --> [E(Rm) - Rf] = m and β = x.

If the correlation, ρ(i, M), is less than one, beta is still some value given by ρ(i,M) * σ(i)/σ(M) such that, in the SML at least, the correlation param informs your location on the X-axis via informing beta. You might be thinking about the interim step before the capital market line (CML). The CML is also linear but plots expected return against volatility and, prior to the introduction of the risk-free asset, the portfolio possibilities curve (PPC) is a curve when correlation is less than zero. Please see my video at https://forum.bionicturtle.com/thre...strates-the-benefit-of-diversification.21442/

 

[Amierul]

Hi @David Harper CFA FRM Thank you very much! But I have another question pls..
would appreciate if u can help to enlighten me..

With reference to below two equations, when moving from efficient frontier to "addition of risk free assets", these two equations are correct.

Assuming Expected return of Investment C that contains risky assets + risk free assets with their corresponding weights, by logic it is given by the left equation.

But based on the right equation, which is the cml equation line, why there are no weightage associated?

 

[David Harper CFA FRM]

Hi @Amierul I think weight is just implicit in the (right-hand) CML where the slope of the CML is the Sharpe ratio of the market portfolio, [E(Rm) - Rf]/σ(M). So, the implicitly the weight to the market portfolio is σ(P)/σ(M); e.g., if σ(P)/σ(M) = 0.70 then 70% weight to market portfolio and remainder 30% weight to riskfree. So weight of [1 - σ(P)/σ(M)] to risk-free asset. Your notation is a bit different than mine, as you don't have market on the right. I'm not sure it's a productive exercise, to be honest. Better to understand deeply the SML versus CML. Or, in the XLS, you can really play with it concretely.

 

[Amierul]

Thank you @David Harper CFA FRM, that has answered my question. It does help me to have concrete understanding about the CML Now.
Yes it is not a productive exercise but ur explanation does not contain inn any book specifically about the Weight of market protflio = σ(P)/σ(M) and the weight of risk-free asset = [1 - σ(P)/σ(M)] which is weird.. even in kaplan schweser.

I am now a bit confident to play around with the XLS. Thanks you!

 

[kc]

Hi @Nicole Seaman, can you please help restore the excel used in the video? Thank you so much!

 

[Nicole Seaman]

Hi @Nicole Seaman, can you please help restore the excel used in the video? Thank you so much!

@kc I've updated the XLS link. Please let me know if you have trouble opening it. Thank you.