GARP.FRM.PQ.P2 Surplus Value GARP 2015 Question 5 (garp15-p2-5)

[CYLoh]

This might be a stupid question, but I just gotta clarify!

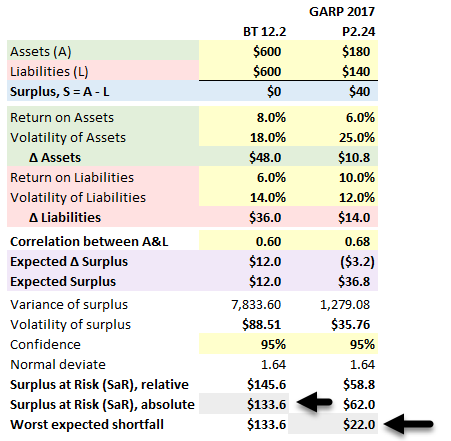
5. An analyst reports the following fund information to the advisor of a pension fund that currently invests in government and corporate bonds and carries a surplus of USD 10 million:

Pension Assets Pension Liabilities
Amount (in USD million) 100 90
Expected Annual Growth 6% 7%
Modified Duration 12 10
Annual Volatility of Growth 10% 5%

To evaluate the sufficiency of the fund's surplus, the advisor estimates the possible surplus values at the end of one year. The advisor assumes that annual returns on assets and the annual growth of the liabilities are jointly normally distributed and their correlation coefficient is 0.8. The advisor can report that, with a confidence level of 95%, the surplus value will be greater than or equal to:

a. USD -11.4 million
b. USD -8.3 million
c. USD -1.7 million
d. USD 0 million

Correct Answer: c

Rationale: The lower bound of the 95% confidence interval is equal to: Expected Surplus - (95% confidence factor * Volatility of Surplus). The required variables can be calculated as follows:
Variance of the surplus = 100^2 * 10%^2 + 90^2 * 5%^2 - 2 * 100 * 90 * 10% * 5% * 0.8 = 48.25
Volatility of the surplus = √48.25 = 6.94,
The expected surplus = 100 * 1.06 - 90 * 1.07 = 9.7.
Therefore, the lower bound of the 95% confidence interval = 9.7 - 1.645 * 6.94 = -1.725

Why is the variance of the surplus calculated as 100^2 * 10%^2 + 90^2 * 5%^2 - 2 * 100 * 90 * 10% * 5% * 0.8
and not 100^2 * 10%^2 + 90^2 * 5%^2 + 2 * 100 * 90 * 10% * 5% * 0.8.

Regards

 

[ShaktiRathore]

Hi
Surplus is given by
s=Assets(A)-Liabilities(L)=A-L
Take variance on both sides,
Var(s)=Var(A-L)=Var(A)+Var(L)-2*Cov(A,L)[we know that Var(a-b)= Var(a)+Var(b)-2*Cov(a,b)]
Var(s)=Var(A-L)=Var(A)+Var(L)-2*rho(A,L)*vol A*vol L[we know Cov(a,b)= rho(a,b)*vol a*vol b]
As Volatilities are expressed in dollars so, vol A=%vol of A*value A, vol L=%vol of L*value L
Var(s)=Var(A-L)=( %vol of A*value A )^2 + ( %vol of L*value L )^2-2*rho(A,L)* %vol of A*value A, * %vol of L*value L
Thanks

 

[Bester]

Hi,

Is the surplus value (lower bound of the 95% confidence interval) in this question not the same as absolute SaR. Also why in this question is the Expected Surplus set equal to 9.7 only?

If I calculate the absolute SaR then the calculation in my view would be as follow:

Expected Surplus - (95% confidence factor *Volatility of Surplus) = 19.7 - (1.645*6.94) = 8.3
where Expected Surplus is 19.7 (100 - 90 + 9.7) ---- not 9.7 as per answer below
and
Variance of the surplus = 1002 * 10%2 + 902 * 5%2 - 2 * 100 * 90 * 10% * 5% * 0.8 = 48.25
Volatility of the surplus = √48.25 = 6.94 (same as answer below)


Question:
An analyst reports the following fund information to the advisor of a pension fund that currently invests in government and corporate bonds and carries a surplus of USD 10 million:

Pension Assets = 100 Pension Liabilities = 90 Amount (in USD million)

Expected Annual Growth 6% for Assets and 7% for Liabilities

Modified Duration 12 for Assets and 10 Liabilities

Annual Volatility of Growth 10% for Assets and 5% for Liabilities

To evaluate the sufficiency of the fund's surplus, the advisor estimates the possible surplus values at the end of one year. The advisor assumes that annual returns on assets and the annual growth of the liabilities are jointly normally distributed and their correlation coefficient is 0.8. The advisor can report that, with a confidence level of 95%, the surplus value will be greater than or equal to:

a. USD -11.4 million
b. USD -8.3 million
c. USD -1.7 million
d. USD 0 million

Correct Answer: c

Rationale: The lower bound of the 95% confidence interval is equal to: Expected Surplus - (95% confidence factor *Volatility of Surplus).
The required variables can be calculated as follows:

Variance of the surplus = 1002 * 10%2 + 902 * 5%2 - 2 * 100 * 90 * 10% * 5% * 0.8 = 48.25
Volatility of the surplus = √48.25 = 6.94,
The expected surplus = 100 * 1.06 - 90 * 1.07 = 9.7.
Therefore, the lower bound of the 95% confidence interval = 9.7 - 1.645 * 6.94 = -1.725

 

[Matthew Graves]

Not sure I follow your calculation of the expected surplus. Your calculation seems to assume that you would be receiving at the end of the year another 100*1.06 assets with additional liabilities of 90*1.07, giving total assets of 206 and total liabilities of 186.3 with a surplus of 19.7.

The question only specifies that the assets and liabilities increase by the respective growth rates, hence at the end of the year assets = 106 and liabilities = 96.3 for a surplus of 9.7, as in the answer.

 

[Bester]

Hi thanks for the response.

How I calculated the Expected Surplus is as follow. Before any growth in the 1st year the surplus is 100 - 90 = 10. Then the assets and liabilities grow by the respective growth rates (106 - 96.3= 9.7). Thus the total new expected surplus (including growth) is 10 + 9.7 = 19.7. This is similar to the example in the Bionic Turtle study notes. See example page 24 Bionic Turtle notes on Jorion Portfolio Risk.

 

[David Harper CFA FRM]

Hi @Bester The question gives expected annual growth of assets as 6% and expected annual growth of liabilities as 7%, so the expected dollar growth of assets is 6%*$100 = +6.0 and the expected dollar growth of liabilities is 7%*90 = +6.30, so the expected surplus at the end of the year = current surplus + change in surplus = $10 + (6 - 6.3) = $10 - 0.3 = $9.7 million. The situation here is:

• Let S = surplus = assets - liabilities, such that current S = 100 - 90 = +10 mm
  
• expected S at end of the year = expected end-of-year assets - expected end-of-year liabilities = (100*1.06) - (90 * 1.07) = 106 - 96.3 = 9.7 mm
• 95% relative surplus as risk; i.e., worst expected loss relative to expected surplus at end of year = 6.95*1.645 ~= 11.43
• 95% absolute SaR = 9.7 - 11.43 = -1.725, per the answer.
  
• However, there is a longstanding definitional ambiguity with respect to SaR: it is valid also to define SaR as -0.3 - 11.43 = -11.73, as this represents the worst expected loss in surplus relative to our initial surplus of +$10.

 

[Arnaudc]

Hi all,
This is probably a really dumb question but why in this formula:
Variance of the surplus = 1002 * 10%2 + 902 * 5%2 - 2 * 100 * 90 * 10% * 5% * 0.8 = 48.25
do use the "-" sign?
In all the VaR formula for 2 assets we have VaR² A + VaR² B "+" CorrAB x VaR A x VaR B
Could someone explain what am I missing here?

 

[Nicole Seaman]

Hi all,
This is probably a really dumb question but why in this formula:
Variance of the surplus = 1002 * 10%2 + 902 * 5%2 - 2 * 100 * 90 * 10% * 5% * 0.8 = 48.25
do use the "-" sign?
In all the VaR formula for 2 assets we have VaR² A + VaR² B "+" CorrAB x VaR A x VaR B
Could someone explain what am I missing here?

Hello @Arnaudc

Please notice that I moved your question here to this thread, where this has been discussed above

Nicole

 

[Arnaudc]

@Nicole Seaman ,
Thank you Nicole.
Furthermore, I found my answer in a nice video made by David:

This is because we are looking at a difference and not an addition as we usually do with VaR of 2 assets... Excellent to realize that before the exam

 

[bpdulog]

5. An analyst reports the following fund information to the advisor of a pension fund that currently invests in government and corporate bonds and carries a surplus of USD 10 million:

Pension Assets Pension Liabilities
Amount (in USD million) 100 90
Expected Annual Growth 6% 7%
Modified Duration 12 10
Annual Volatility of Growth 10% 5%

To evaluate the sufficiency of the fund's surplus, the advisor estimates the possible surplus values at the end of one year. The advisor assumes that annual returns on assets and the annual growth of the liabilities are jointly normally distributed and their correlation coefficient is 0.8. The advisor can report that, with a confidence level of 95%, the surplus value will be greater than or equal to:

a. USD -11.4 million
b. USD -8.3 million
c. USD -1.7 million
d. USD 0 million
Correct Answer: c
Rationale: The lower bound of the 95% confidence interval is equal to: Expected Surplus - (95% confidence factor * Volatility of Surplus). The required variables can be calculated as follows:
Variance of the surplus = 1002 * 10%2 + 902 * 5%2 - 2 * 100 * 90 * 10% * 5% * 0.8 = 48.25
Volatility of the surplus = √48.25 = 6.94,
The expected surplus = 100 * 1.06 - 90 * 1.07 = 9.7.
Therefore, the lower bound of the 95% confidence interval = 9.7 - 1.645 * 6.94 = -1.725


Hi,

Does any one know why the third term in the surplus variance formula is being subtracted? This is usually added.

 

[Nicole Seaman]

5. An analyst reports the following fund information to the advisor of a pension fund that currently invests in
government and corporate bonds and carries a surplus of USD 10 million:
Pension Assets Pension Liabilities
Amount (in USD million) 100 90
Expected Annual Growth 6% 7%
Modified Duration 12 10
Annual Volatility of Growth 10% 5%
To evaluate the sufficiency of the fund's surplus, the advisor estimates the possible surplus values at the end
of one year. The advisor assumes that annual returns on assets and the annual growth of the liabilities are
jointly normally distributed and their correlation coefficient is 0.8. The advisor can report that, with a
confidence level of 95%, the surplus value will be greater than or equal to:
a. USD -11.4 million
b. USD -8.3 million
c. USD -1.7 million
d. USD 0 million
Correct Answer: c
Rationale: The lower bound of the 95% confidence interval is equal to: Expected Surplus - (95% confidence factor *
Volatility of Surplus). The required variables can be calculated as follows:
Variance of the surplus = 1002 * 10%2 + 902 * 5%2 - 2 * 100 * 90 * 10% * 5% * 0.8 = 48.25
Volatility of the surplus = √48.25 = 6.94,
The expected surplus = 100 * 1.06 - 90 * 1.07 = 9.7.
Therefore, the lower bound of the 95% confidence interval = 9.7 - 1.645 * 6.94 = -1.725
Section: Risk Management and Investment Management
Reference: Philippe Jorion, Value-at-Risk: The New Benchmark for Managing Financial Risk, 3rd Edition, Chapter 17,
“VaR and Risk Budgeting in Investment Management.”
Learning Objective: Distinguish among the following types of risk: absolute risk, relative risk, policy-mix risk, active
management risk, funding risk, and sponsor risk.


Hi,

Does any one know why the third term in the surplus variance formula is being subtracted? This is usually added.

Hello @bpdulog

Please note that I have moved your question here to this thread, where this question is already being discussed. Please make sure to use our search box, and search for the first sentence in the question before posting a new thread somewhere else in the forum. Many times, these questions have already been posted in the forum. This helps to keep our forum organized and uncluttered so our members can search for answers to their questions easily without having to read through a bunch of different threads on the same question.

Thank you,

Nicole

 

[David Harper CFA FRM]

@bpdulog because surplus = assets - liabilities, not asset + liabilities, so this is an application of variance(A-B) or in this case variance(S) = variance (A -L) = variance(A) + variance(L) - 2*σ(A)*σ(L)*ρ(A,L). I hope that explains!

 

[raghav159]

@David Harper CFA FRM @Nicole Seaman A Similar Question appeared in 2018 Practice but the Z-Normal Deviate used in the solution was 2-tailed. Having difficulty understanding whether it should be a 1-tailed or 2-tailed CI for 95% Surplus . To make things worse the choices have options for both 1-tailed & 2-tailed deviates.


Q. 24 An analyst reports the following fund information to the advisor of a pension fund that currently invests in government and corporate bonds and carries a surplus of USD 40 million:

Assets - 180 million Growth 6% Volatility 25%
Liabilities - 140 million Growth 10% Volatility 12%

To evaluate the sufficiency of the fund's surplus, the advisor estimates the possible surplus values at the end of 1 year. The advisor assumes that annual returns on assets and the annual growth of the liabilities are jointly normally distributed and their correlation coefficient is 0.68. Assume that the volatility of surplus in dollar is USD 35.76 million, what is the lower bound of the 95% confidence interval for the expected end-of-year surplus that the advisor can report?

A) -$ 76.4 million
B) - $ 58.2 million
C) -$ 33.3 million
D) -$ 22 million

Correct Answer : C

C is correct. The lower bound of the 95% confidence interval is equal to: Expected Surplus – (95% confidence factor * Volatility of Surplus).

Explanation:
Expected surplus:
VA*[1 + E(RA)] – VL*[1 + E(RL)] = 180*1.06 – 140*1.10 = USD 36.80 million.
For a 95% confidence interval, the appropriate z-value is 1.96. Therefore, the lower bound of the surplus at the 95% confidence level = 36.80 – 1.96*35.76 = USD -33.2896 million.


Is there really a difference between

2015 - "The advisor can report that, with a confidence level of 95%, the surplus value will be greater than or equal to" => 1-tailed &
"
2018 - " what is the lower bound of the 95% confidence interval for the expected end-of-year surplus that the advisor can report?" => 2-tailed

 

[David Harper CFA FRM]

Hi @raghav159 I think you are looking at incorrect version of the question. We supplied GARP with a correction such that the most recent version's answer is about 22 million (the practice papers have many mistakes in them; the 2018 practice paper issued three revisions and it still has problems).

In regard to your basic question, value at risk is always one-tailed, whether parametric (scaled sigma) or stressing the spread in LVaR, or here in SaR. if it's a "normal (normally distributed) with 95% confidence," the deviate is always 1.645 or 1.65. We've seen many variations and requests for exceptions, yet there has never been a single exception! VaR is about the loss tail ....

The 2018 practice paper is merely a recycled, corrected version of the 2017 paper, so this 2018.P2.24 is an update/revision of 2017.P2.24 which we discussed here at (paid subscribers only)
https://forum.bionicturtle.com/threads/p2-t8-12-surplus-at-risk-sar-jorion.5488/post-50372
i.e.,

Hi @FrmL2_Aspirant Yes, that's a sharp comparison (ie, between the above 12.2 and GARP's 2017 P2.24). Please note my comparison below (XLS here for future reference [link for paid subscribers only). This is an issue we are familiar with. Please notice the approaches are not really different; i.e., both approaches utilize VaR(A-L) and ρ(A,L) to infer surplus volatility. The "issue" is related to the distinction between relative and absolute VaR, except that surplus at risk has three valid answers depending on the reference point. Using GARP 2017 P2.24 as an example:

• Relative SaR is worst expected loss relative to the future expected surplus; as usual, it is simply scaled surplus volatility, in this case $35.76 * 1.645 = $58.8 mm
• Absolute SaR is worst expected loss relative to initial surplus; in this case, -(-3.2) + $35.76 * 1.645 = $62.0. In words, only 5% should the surplus decline more than $62.0 mm from its current position which is $40.0
• Worst expected shortfall is worst expected loss relative to zero surplus; in this case, per the solution given: +36.8 mm expected surplus - ($35.76 * 1.645) = -$22.0 mm; note my calcs treat losses as positives, but it's the same result.

Those are my adopted terms, and I continue to give GARP feedback on this (they have asked me to review the revised PQ practice paper) but notice the language of the question is "The advisor can report that, with a confidence level of 95%, the surplus value will be greater than or equal to" which I think is an accurate phrasing of what I would call worst expected shortfall. My current feedback will include the suggestion that an additional phrase be added to be super careful around the negative/positive usage. (-22.0 is totally understandable but I think some of us are consistent by deriving +22.0, so it's just important to be clear in the question!). These SaR questions are tricky, I hope that at least clarifies how the approach is not really different.

 

[raghav159]

@David Harper CFA FRM Dear David,
Thanks for the prompt response. I do see some corrections in 2018 paper compared to 2017, however the answer to this question is still Incorrect. I have downloaded the latest edition of the 2018 practice paper from the Garp website
https://my.garp.org/sfdcApp#!/study_materials
Is there any other link to download the revised version?

 

[David Harper CFA FRM]

@raghav159 I don't think you have the latest (it could be their glitch. GARP's nonchalant approach to the Practice Papers has been very discouraging to many of us). They've had many errors and corrections, so maybe the error reverted. Below is my version. I don't have any other links to share for non-subscribers, sorry.

 

[Gareth]

This question is around the Surplus loss quantile. The same question appears in the 2017 and 2018 past papers, but one uses z = 1.96 and the other z = 1.645 for the 95% confidence. Surely this is a one-tailed test?

Or is it a mistake by GARP? Would appreciate any quick responses given the exam being tomorrow, but of course appreciate everybody's time is at a premium now.

Thanks

2018:

An analyst reports the following fund information to the advisor of a pension fund that currently invests in government and corporate bonds and carries a surplus of USD 40 million:

Pension Assets Liabilities Amount (USD million) 180 140
Expected annual growth rate 6% 10%
Annual volatility of growth rates 25% 12%

To evaluate the sufficiency of the fund's surplus, the advisor estimates the possible surplus values at the end of 1 year. The advisor assumes that annual returns on assets and the annual growth of the liabilities are jointly normally distributed and their correlation coefficient is 0.68. Assume that the volatility of surplus in dollar is USD 35.76 million, what is the lower bound of the 95% confidence interval for the expected end-of-year surplus that the advisor can report?

A. USD -76.4 million
B. USD -58.2 million
C. USD -33.3 million
D. USD -22.0 million

Correct Answer: C
Explanation: C is correct. The lower bound of the 95% confidence interval is equal to: Expected Surplus – (95% confidence factor * Volatility of Surplus). Expected surplus: VA*[1 + E(RA)] – VL*[1 + E(RL)] = 180*1.06 – 140*1.10 = USD 36.80 million. For a 95% confidence interval, the appropriate z-value is 1.96. Therefore, the lower bound of the surplus at the 95% confidence level = 36.80 – 1.96*35.76 = USD -33.2896 million.

2017:

Formatting messes up when I post it but its the same calc but 1.645. Which seems correct to me.

Thanks

 

[Nicole Seaman]

This question is around the Surplus loss quantile. The same question appears in the 2017 and 2018 past papers, but one uses z = 1.96 and the other z = 1.645 for the 95% confidence. Surely this is a one-tailed test?

Or is it a mistake by GARP? Would appreciate any quick responses given the exam being tomorrow, but of course appreciate everybody's time is at a premium now.

Thanks

2018:

An analyst reports the following fund information to the advisor of a pension fund that currently invests in government and corporate bonds and carries a surplus of USD 40 million:

Pension Assets Liabilities Amount (USD million) 180 140
Expected annual growth rate 6% 10%
Annual volatility of growth rates 25% 12%

To evaluate the sufficiency of the fund's surplus, the advisor estimates the possible surplus values at the end of 1 year. The advisor assumes that annual returns on assets and the annual growth of the liabilities are jointly normally distributed and their correlation coefficient is 0.68. Assume that the volatility of surplus in dollar is USD 35.76 million, what is the lower bound of the 95% confidence interval for the expected end-of-year surplus that the advisor can report?

A. USD -76.4 million
B. USD -58.2 million
C. USD -33.3 million
D. USD -22.0 million

Correct Answer: C
Explanation: C is correct. The lower bound of the 95% confidence interval is equal to: Expected Surplus – (95% confidence factor * Volatility of Surplus). Expected surplus: VA*[1 + E(RA)] – VL*[1 + E(RL)] = 180*1.06 – 140*1.10 = USD 36.80 million. For a 95% confidence interval, the appropriate z-value is 1.96. Therefore, the lower bound of the surplus at the 95% confidence level = 36.80 – 1.96*35.76 = USD -33.2896 million.

2017:

Formatting messes up when I post it but its the same calc but 1.645. Which seems correct to me.

Thanks

Hello @Gareth

I moved your question to this thread, which discusses this practice question (note the thread begins with a PQ that is similar, but this specific question is discussed further down in the comments).

Thank you,

Nicole

 

[Gareth]

Thanks!

 

[anisapassfrm]

David, I think the expected surplus should be 100*0.06-90*0.07

Hi @Bester The question gives expected annual growth of assets as 6% and expected annual growth of liabilities as 7%, so the expected dollar growth of assets is 6%*$100 = +6.0 and the expected dollar growth of liabilities is 7%*90 = +6.30, so the expected surplus at the end of the year = current surplus + change in surplus = $10 + (6 - 6.3) = $10 - 0.3 = $9.7 million. The situation here is:

• Let S = surplus = assets - liabilities, such that current S = 100 - 90 = +10 mm
• expected S at end of the year = expected end-of-year assets - expected end-of-year liabilities = (100*1.06) - (90 * 1.07) = 106 - 96.3 = 9.7 mm
• 95% relative surplus as risk; i.e., worst expected loss relative to expected surplus at end of year = 6.95*1.645 ~= 11.43
• 95% absolute SaR = 9.7 - 11.43 = -1.725, per the answer.
• However, there is a longstanding definitional ambiguity with respect to SaR: it is valid also to define SaR as -0.3 - 11.43 = -11.73, as this represents the worst expected loss in surplus relative to our initial surplus of +$10.