Kavita.bhangdia
Active Member
Hello everyone,
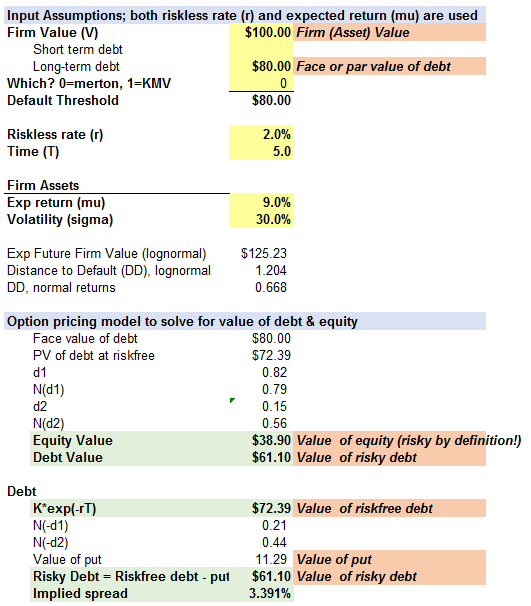
I had thought that I had sorted it out, but today I was reading the Merton model again but am completely lost with the difference between risky debt and risk free debt. Please can someone redefine it
Risky debt = riskfree debt-put option..
Please explain risky and risk free debt.
Thanks
Kavita
I had thought that I had sorted it out, but today I was reading the Merton model again but am completely lost with the difference between risky debt and risk free debt. Please can someone redefine it
Risky debt = riskfree debt-put option..
Please explain risky and risk free debt.
Thanks
Kavita