gargi.adhikari
Active Member
In Reference to R20.P1.T3.FIN_PRODS_McDonald_Ch6_Topic: Cash_Flows_Arbitrage Transaction in Commodity Forwards:-
Hi,
I having some trouble wrapping my head around the Cash Flow depicted below:-
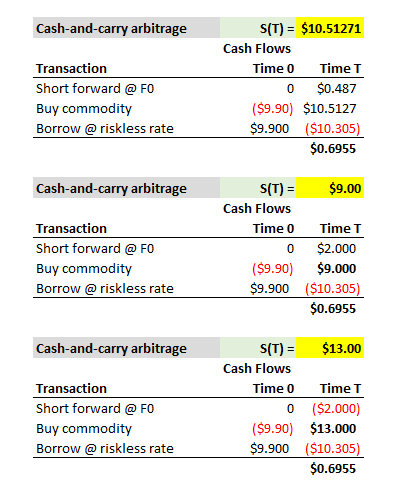
The Short Forward Payoff is ( K-St)= ( 11- 10.5127) So the money that we spent in buying the Spot is getting accounted for when we subtract St from K and get the effective Payoff= (K- St)
But to get the Net of .6955 = [ ( .48 + 10.5127 ) - 10.305 ] So we are adding back St(10.5127) to the Net. So effectively Net= [ (K- E[S(t) ] ) + E[S(t) ] - S0.e^-(r- lease rate).T ]
So, effectively, we are not accounting for the fact that we paid E[S(t) ] (= S0. e^ growthRate.T) to buy the Spot....?
Hi,
I having some trouble wrapping my head around the Cash Flow depicted below:-
The Short Forward Payoff is ( K-St)= ( 11- 10.5127) So the money that we spent in buying the Spot is getting accounted for when we subtract St from K and get the effective Payoff= (K- St)
But to get the Net of .6955 = [ ( .48 + 10.5127 ) - 10.305 ] So we are adding back St(10.5127) to the Net. So effectively Net= [ (K- E[S(t) ] ) + E[S(t) ] - S0.e^-(r- lease rate).T ]
So, effectively, we are not accounting for the fact that we paid E[S(t) ] (= S0. e^ growthRate.T) to buy the Spot....?


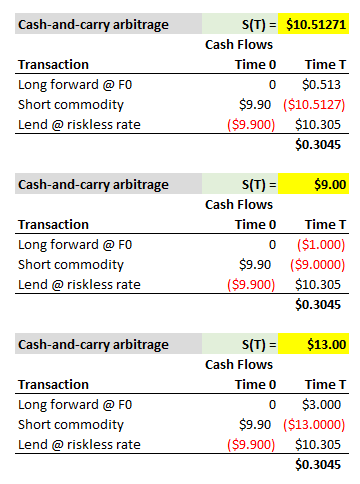
 You are correct that under the cash and carry (i.e., sell the trading-expensive forward and buy the trading-cheap commodity) in the future we do not buy the commodity (because we already did today). Below I copied this scenario below but with three different future (commodity) spot prices to show that--just as your formula shows--the future spot commodity price does not matter (this is an arbitrage: it must guarantee a profit regardless of the future spot price!). In the notes, I followed McDonald by illustrating a future spot price that just happens to be realized as the expected future spot price; but it cancels out in the future cash flow. (my xls is here @
You are correct that under the cash and carry (i.e., sell the trading-expensive forward and buy the trading-cheap commodity) in the future we do not buy the commodity (because we already did today). Below I copied this scenario below but with three different future (commodity) spot prices to show that--just as your formula shows--the future spot commodity price does not matter (this is an arbitrage: it must guarantee a profit regardless of the future spot price!). In the notes, I followed McDonald by illustrating a future spot price that just happens to be realized as the expected future spot price; but it cancels out in the future cash flow. (my xls is here @  ... and sort of zen. How so? First, we borrow everything we need to buy the (spot) commodity; hence the cash inflow (borrowing) to fund the purchase of the commodity. Second, simultaneously, we enter the short forward contract (with zero cost).
... and sort of zen. How so? First, we borrow everything we need to buy the (spot) commodity; hence the cash inflow (borrowing) to fund the purchase of the commodity. Second, simultaneously, we enter the short forward contract (with zero cost).