Practice question 3 - Backtesting VaR

[ami44]

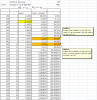
Hi,

Practice Question number 3 in the GARP Market Risk reading goes like this:

You are backtesting a bank's VaR model. Currently, the bank calculates a 1-day VaR at the 99% confidence level, and you are recommending that it switch to a 95% confidence level. Which of the following statements concerning this switch is correct?

A. The 95% VaR model is less likely to be rejected using backtesting than the 99% VaR model.

B. When validating with backtesting at the 90% confidence level, there is smaller probability of incorrectly rejecting a 95% VaR model when it is valid than a 99% VaR model.

C. The decision to accept or reject a VaR model based on backtesting results is more reliable with a 95% confidence level VaR model than with a 99% confidence level VaR model

D. When backtesting using a 90% confidence level, there is a smaller probability of committing a type 1 error when backtesting a 95% VaR model than with a 99% VaR model.

The official answer is C.

I agree that C is correct. But aren't B and D also correct?
In fact isn't B and D together the same as C, i.e. the decision is more reliable, since the probability of making an error (type 1 or 2) is smaller.
Is the question just weird, or do I miss something here?

 

[ShaktiRathore]

Hi
Type I error is equal to significance level=1-CL.
Our hypothesis test for model is:Ho:model is correct and Ha:model is incorrect
95% model has type I error probability as 5% is more probable to reject model(reject Ho) than 99%model whose type I error is 1% . It follows A and B and D re incorrect
Whats left C is correct. I think more type II errors creeps in for 99% model than 95% model so probability of accepting an incorrect model is less for 95% model so is more efficient than 99% model.
Thanks

 

[ami44]

Shakti, thank you for your reply.

The confidence level for the backtesting is in both cases 90%. But one time a 99% VaR and the other time a 95% VaR is backtestet.

 

[ShaktiRathore]

Hi
Yes in 90% CL for 100 observations we have no of exceptions>10 to correctly reject the model ,if 5<no of exceptions<=10 we incorrectly accept the 95%Var model at 90%cl leading type II error and if 1<no of exceptions<=10 we incorrectly accept the 99% model at 90%cl ,from above its clear that probability of type II error is more for 99% CL than 95% CL,therefore 95% model is more reliable. Also there is a tradeoff bw typeI and type II errors means more type I error leads to less type II error and vise versa.Since prob typeII is more for 99% CL than 95% CL therefore prob of type I is more for 95% model than 99% model.
Thanks

 

[John Le]

hi, everyone!
i am also interested in this topic. so i have 2 questions on backtesting procedure:

1) The basel backtesting procedure implicitly tests the following hypothesis:
H0 : P= P0 Vs Ha : P >P0 ( here P0 = 0.01)
based on sample of 250 observation, 99% confident level. i understand the way they calculate outcome of collumn "exact", and collumn Type I error (pls see the attached file)

Question 1: i dont understand why Basel committee choose "threshold is K= 10 exceptions" as barrier to distinguish "reject or accept" H0? why they dont choose another number such as 11, 12 th where we can see that the probability of Type 1 error is smaller 0.005% and 0.001% respectively ( P(X>=11) =0.005%; P(X>=12= 0.001% instead of P(X>=10) =0.03%) ????

And the similar questions for Greeen zone and yellow zone in Basel II

2) I just have read about Standard Coverage testing at the link follows:

http://www.value-at-risk.net/backtesting-coverage-tests/,

one of its paragraph said that: "Suppose we implement a one-day 95% VaR measure and plan to backtest it at the .05 significance level after 500 trading days (about two years). Then q = 0.95 and α + 1 = 500. Assuming

, we know X ~ B(500, .05). We use this distribution to determine x1 = 15 and x2 = 36. Calculations are summarized in Exhibit 14.2. We will reject the VaR measure if X ∉ [16, 35]"

Question 2: is how can i determint x1, x2 as 15, 36 respectively. I dont know why they can figure out that number?

Thank you all of you, i am looking forward to seeing your helps

 

[David Harper CFA FRM]

Hi @John Le

Question #1 is a good one! You may want to look at Annex 10 of the Basel II Framework (it's a huge document, so it's easy to miss this excellent explainer) here at https://www.dropbox.com/s/ehrzuwv1uqtef88/b2-framework-backtest-annex.pdf?dl=0. The answer is the classic trade-off: you are correct that increasing the threshold would lower the probability of a Type I error, but given the same sample size, it would also necessarily increase the probability of a Type II error (i.e., inadvertently accepting a bad VaR model). For example (from this Annex):

"33. Under the assumptions that the model’s true level of coverage is not 99%, Table 1 reports the probability that selecting a given number of exceptions as a threshold for rejecting the accuracy of the model will result in an erroneous acceptance of a model with the assumed (inaccurate) level of coverage (“type 2” error). For example, if the model’s actual level of coverage is 97%, and the threshold for rejection is set at seven or more exceptions, the table indicates that this model would be erroneously accepted 37.5% of the time."

In regard to Question #2, it looks like the author simply computing the probability for each left/right tail and combined them (i.e., two tailed rejection region) so they summed near to 5.0%. That is, using Excel

• P (X < 16) = binom.dist(X = 15, 500 trials, 5% probability, true = CDF) = 0.0199 is the probability of 15 or fewer exceedences over 500 trials if it is a 95% VaR model
• P (X > 34) = 1 - binom.dist(X = 34, 500, 5%, true) = 0.0303
• P (X < 16) + P (X > 34) = 0.0199 + 0.0303 = 0.0501, is the two-tailed rejection region. I hope that helps!

 

[John Le]

Thank for your quick reply!

i also agree with you that All statistical hypothesis tests have a probability of making type I and type II errors, we have to trade off against each other (type 1, type 2): for any given sample set, the effort to reduce one type of error generally results in increasing the other type of error.

1) What is criteria for "trade off" that persuade us is reasonable? 0.03% and 99.97% (10th) VS 0.4% and 99.6% (8th) ? if i dont misunderstand, basel II backtest is not designed to control the Type II error rate ?


2) From my point of view, i am still wondering about the way Basel II choose "the threshold", in my opinion: i prefer to choose the threshold (red zone is from K = equal to greater than 8 exceptions), the reason persuades me that:
The type I error rate or significance level is the probability of rejecting the null hypothesis (H0) given that it is true

By convention, the significance level is set to 0.01 (1%), implying that it is acceptable to have a 1% probability of incorrectly rejecting the null hypothesis (H0) ----> look at 8th exception , we see probability of Type 1 is 0.4% ( we can't choose the next one above 8th (1.37%) which is greater than 1%)

My Question: can I choose Red Zone is from equal to and greater than 8 exceptions? ( it seems to be less conservative than Basel II threshold?)



tks, Thái

 

[David Harper CFA FRM]

Hi @John Le I encourage you to read the Basel Committee's justification for the backtest zones; it anticipates, I think, part of your observation. First, please note, eight (8) exceedences is, indeed, in the yellow zone. As the document says (emphasis mine), "The green zone corresponds to backtesting results that do not themselves suggest a problem with the quality or accuracy of a bank’s model. The yellow zone encompasses results that do raise questions in this regard, but where such a conclusion is not definitive. The red zone indicates a backtesting result that almost certainly indicates a problem with a bank’s risk model."

Second, of course you are correct that 0.01 (and 0.05) are conventional. But, as Gujarati says somewhere, there is nothing sacrosanct about 1% and 5%; the appropriate significance level depends on the consequences of the errors. And, in this case, they are especially concerned with a Type II error. It is important, here, I think, to keep in mind that failure to reject a null does not imply acceptance of the null. And, in this context, the committee is very concerned about the Type II error; i.e., mistakenly "accepting" a bad VaR model.

Third, and related, you are not showing the probability of Type II errors. A Type I error is very specific mistake: the probability of rejecting the model conditional on the VaR model being accurate. See the document's (Annex 10a, above) Table 1. What is the probability of a Type II error if the Var model is 97.0% accurate (instead of the assumed 99.0%) and if we observe (your number) eight exceptions? This probability is fully 52.4%. That's why the committee, I expect, set the red zone higher. I hope this helps!

From Annex 10a (emphasis mine):

"29. Three zones have been delineated and their boundaries chosen in order to balance two types of statistical error: (1) the possibility that an accurate risk model would be classified as inaccurate on the basis of its backtesting result, and (2) the possibility that an inaccurate model would not be classified that way based on its backtesting result.
30. Table 1 reports the probabilities of obtaining a particular number of exceptions from a sample of 250 independent observations under several assumptions about the actual percentage of outcomes that the model captures (that is, these are binomial probabilities). For example, the left-hand portion of Table 1 reports probabilities associated with an accurate model (that is, a true coverage level of 99%). Under these assumptions, the column labelled “exact” reports that exactly five exceptions can be expected in 6.7% of the samples.
31. The right-hand portion of Table 1 reports probabilities associated with several possible inaccurate models, namely models whose true levels of coverage are 98%, 97%, 96%, and 95%, respectively. Thus, the column labelled “exact” under an assumed coverage level of 97% shows that five exceptions would then be expected in 10.9% of the samples.
32. Table 1 also reports several important error probabilities. For the assumption that the model covers 99% of outcomes (the desired level of coverage), the table reports the probability that selecting a given number of exceptions as a threshold for rejecting the accuracy of the model will result in an erroneous rejection of an accurate model (“type 1” error). For example, if the threshold is set as low as one exception, then accurate models will be rejected fully 91.9% of the time, because they will escape rejection only in the 8.1% of cases where they generate zero exceptions. As the threshold number of exceptions is increased, the probability of making this type of error declines.
33. Under the assumptions that the model’s true level of coverage is not 99%, Table 1 reports the probability that selecting a given number of exceptions as a threshold for rejecting the accuracy of the model will result in an erroneous acceptance of a model with the assumed (inaccurate) level of coverage (“type 2” error). For example, if the model’s actual level of coverage is 97%, and the threshold for rejection is set at seven or more exceptions, the table indicates that this model would be erroneously accepted 37.5% of the time.
34. In interpreting the information in Table 1, it is also important to understand that although the alternative models appear close to the desired standard in probability terms (97% is close to 99%), the difference between these models in terms of the size of the risk measures generated can be substantial. That is, a bank’s risk measure could be substantially less than that of an accurate model and still cover 97% of the trading outcomes. For example, in the case of normally distributed trading outcomes, the 97th percentile corresponds to 1.88 standard deviations, while the 99th percentile corresponds to 2.33 standard deviations, an increase of nearly 25%. Thus, the supervisory desire to distinguish between models providing 99% coverage, and those providing say, 97% coverage, is a very real one."

 

[John Le]

Thank David, i will study it carefully.

By the way , i send to you the Probability of Type II type I as the attached file (both C.L 99% and 97%)

Tks

 

[vybnji]

Hi David,
A bit confused as to why below answer is not correct?
A. The 95% VaR model is less likely to be rejected using backtesting than the 99% VaR model.

To my understanding, we are supposed to reject the model if the z value computed below is greater than the value of the confidence level used to back-test the model.
as per the formula z = [x - pT] / [sqrt(p(1-p)T], a higher p value (i.e. level of significance results in a lower z-score), so shouldn't a 95% VaR model be less likely to be rejected than 99% VaR?

Examples below:

using 95% VaR: z = [22 - 0.05(252)] / [sqrt(0.05*0.95*252)] = 2.72
using 99% VaR: z = [22 - 0.01(252)] / [sqrt(0.01*0.99*252)] = 12.33

Therefore, the z-value computed using the 99% VaR is larger and therefore has a higher chance of being greater than the confidence level used to back-test e.g. 1.96, in other words, wouldn't that mean that higher VaR confidence levels result in more rejected models?

 

[David Harper CFA FRM]

Hi @vybnji The fallacy in your comparison is that you assume X = 22 under both VaRs, right!? Consider this as-if historical sequence that I have (sincerely in Excel) randomly generated (µ = 10, σ = 30%) over the past 10 trading days, using =-µ+NORM.S.INV(RAND())*σ: (0.09), (0.41), 0.57, 0.19, (0.06), (0.55), (0.12), (0.30), 0.08, 0.42. So there are all in L(+)/P(-) format. Ex ante, the 95.0% VaR was (and is) -10%*30%*1.65 = 0.39 and there were two (2) exceptions: 0.57 and 0.42 both exceeded the VaR. But the 99.0% VaR is -10%+30%*2.33 = 0.60 and there were zero exceptions in this sample. The sample is unchanged (i.e., the distribution is the same) but the 99.0% VaR must be higher than 95.0% VaR. More technically, as Dowd explains (Chapter 3), "the standard error rises as the probabilities become more extreme and we move further into the tail – hence, the more extreme the quantile, the less precise its estimator." There is more discussion here https://forum.bionicturtle.com/thre...d-errors-of-coherent-risk-measures-dowd.3666/

 

[rishivala]

Hi David,
I am having a hard time why is C correct for this question. The answer says 95% VaR is more "reliable" than 99% VaR. Does that mean its statistical power is higher (1 - probability of Type II Error)?

If the answer is referring to power, then if we assume the true model is 93% and calculate the power, the results contradict the answer. Here is a numerical example. I am calculating the probability of a type II error by assuming the true model is 93% and then finding the cumulative probability of the non-rejection region under 95% VaR model and 99% VaR model.

VaR Confidence Level	95%	99%
Sample Size	100	100
99th percentile on Binomial Distribution	11	4
True model coverage (confidence level)	93%	93%
Probability of Type II error	95.31% [BINOM.DIST(11,100,7%,TRUE)]	16.3% [BINOM.DIST(4,100,7%,TRUE)]
Power (1 - Probability of Type II error)	4.69%	83.7%

 

[David Harper CFA FRM]

Hi @rishivala Right, i mean, setting aside a fact that it appears you already understand power is tricky (ie., this is not the actual power because you conditioned on a true model at 93% b/c that's the best you can do to keep it simple), that's the reason I skipped answering the question: the use of "reliable" is imprecise (aka, lazy) in this context where word accuracy is very important. This looks like an early version of a question that GARP took years to fix, they revised it at least three time and each revision had a new problem. Clearly the writer was not expert on the topic. The moral of the story, to me, is simple: do not get bogged down in bad questions. Here is discussion on one of the iterations (with further link to an excel I made that probably makes a point similar to your point, about power) https://forum.bionicturtle.com/threads/garp-2020-p2-53-and-garp-2019-p2-53.22374/

 

[rishivala]

Hi @rishivala Right, i mean, setting aside a fact that it appears you already understand power is tricky (ie., this is not the actual power because you conditioned on a true model at 93% b/c that's the best you can do to keep it simple), that's the reason I skipped answering the question: the use of "reliable" is imprecise (aka, lazy) in this context where word accuracy is very important. This looks like an early version of a question that GARP took years to fix, they revised it at least three time and each revision had a new problem. Clearly the writer was not expert on the topic. The moral of the story, to me, is simple: do not get bogged down in bad questions. Here is discussion on one of the iterations (with further link to an excel I made that probably makes a point similar to your point, about power) https://forum.bionicturtle.com/threads/garp-2020-p2-53-and-garp-2019-p2-53.22374/

Thanks for the prompt response. I agree this question has areas of improvement, and based on the thread you have linked it seems as though GARP is struggling with landing on a sound question. Glad my logic is not faulty.
Cheers!

 

[xzbest]

Hi @vybnji The fallacy in your comparison is that you assume X = 22 under both VaRs, right!? Consider this as-if historical sequence that I have (sincerely in Excel) randomly generated (µ = 10, σ = 30%) over the past 10 trading days, using =-µ+NORM.S.INV(RAND())*σ: (0.09), (0.41), 0.57, 0.19, (0.06), (0.55), (0.12), (0.30), 0.08, 0.42. So there are all in L(+)/P(-) format. Ex ante, the 95.0% VaR was (and is) -10%*30%*1.65 = 0.39 and there were two (2) exceptions: 0.57 and 0.42 both exceeded the VaR. But the 99.0% VaR is -10%+30%*2.33 = 0.60 and there were zero exceptions in this sample. The sample is unchanged (i.e., the distribution is the same) but the 99.0% VaR must be higher than 95.0% VaR. More technically, as Dowd explains (Chapter 3), "the standard error rises as the probabilities become more extreme and we move further into the tail – hence, the more extreme the quantile, the less precise its estimator." There is more discussion here https://forum.bionicturtle.com/thre...d-errors-of-coherent-risk-measures-dowd.3666/

Hi David!
I am a little confused about VaR testing.
Let's assume
Model 1: 99% VaR, at the 95% confidence level,
Model 2: 95% VaR, at the 95% confidence level,
Model 3: 95% VaR, at the 90% confidence level.

Question 1: Is Model 2 more reliable than Model 1, because Model 2 is more likely to be rejected?
Question 2: Is the probability of type I error of Model 1 same as Model 2, since α of both models is 5%?
Question 3: How to compare the probability of type II error (β) of three models?

Thanks a lot!

 

[David Harper CFA FRM]

Hi @xzbest

Question 1: Is Model 2 more reliable than Model 1, because Model 2 is more likely to be rejected?
What exactly is "reliability" in the specific context of hypothesis testing? I'm aware of its connotations in other contexts, but we had to send correction(s) to GARP when they used it two of their practice papers. But those questions had embarrassingly multiple problems. Put another way, GARP's use of reliable has not been reliable. See https://forum.bionicturtle.com/threads/garp-2020-p2-53-and-garp-2019-p2-53.22374/

Question 2: Is the probability of type I error of Model 1 same as Model 2, since α of both models is 5%?
Yes, the significance level is probability of Type I error rate; both M1 and M2 conduct a backtest (hypothesis) test where the significance level is 5.0%. (homework: but they do not have the same cutoffs, why?)

Question 3: How to compare the probability of type II error (β) of three models?
At first glace (I only want to take 5 minutes now), that's hard for me. Beta/power trades off with significance (lower sig = lower T1 error --> higher T2/lower power; aka, higher confidence --> lower power and higher power --> lower confidence). So M3 may have higher power (i.e., lower confidence) than M1-2 but it seems to me comparability in this abstract (no facts) scenario might be totally unjustified; e.g., we do not have sample sizes. Don't want to opine.

Thanks, David

 

[xzbest]

Hi @xzbest

Question 1: Is Model 2 more reliable than Model 1, because Model 2 is more likely to be rejected?
What exactly is "reliability" in the specific context of hypothesis testing? I'm aware of its connotations in other contexts, but we had to send correction(s) to GARP when they used it two of their practice papers. But those questions had embarrassingly multiple problems. Put another way, GARP's use of reliable has not been reliable. See https://forum.bionicturtle.com/threads/garp-2020-p2-53-and-garp-2019-p2-53.22374/

Question 2: Is the probability of type I error of Model 1 same as Model 2, since α of both models is 5%?
Yes, the significance level is probability of Type I error rate; both M1 and M2 conduct a backtest (hypothesis) test where the significance level is 5.0%. (homework: but they do not have the same cutoffs, why?)

Question 3: How to compare the probability of type II error (β) of three models?
At first glace (I only want to take 5 minutes now), that's hard for me. Beta/power trades off with significance (lower sig = lower T1 error --> higher T2/lower power; aka, higher confidence --> lower power and higher power --> lower confidence). So M3 may have higher power (i.e., lower confidence) than M1-2 but it seems to me comparability in this abstract (no facts) scenario might be totally unjustified; e.g., we do not have sample sizes. Don't want to opine.

Thanks, David

Hi David:
Thank you for helping me clear the relationship between model power and confidence level.

Wish u best luck!
xzbest

 

[PKuma9691]

@David Harper CFA FRM , Hello sir. FRM Level 2 sample paper-1 has the following question which is creating confusion. Please help with the solution they have given:

Version:0.9 StartHTML:0000000105 EndHTML:0000004848 StartFragment:0000000141 EndFragment:0000004808
Question
A newly hired risk analyst at a mid-size bank is assisting in backtesting the bank’s
VaR model. Currently, the 1-day VaR is estimated at the 95% confidence level but
the bank is considering a change to estimating 1-day VaR at the 99% confidence
level, as recommended in the Basel framework. Which of the following statements
concerning this change is correct?
A
The decision to accept or reject a VaR model based on the results of a backtest that
uses a two-tailed 95% confidence level is less reliable when applied to a 99% VaR
model than when applied to a 95% VaR model.
B
The 95% VaR model is less likely to be rejected by a backtest than the 99% VaR
model.
C
When using a two-tailed 90% confidence level test in a backtest, there is a smaller
probability of incorrectly rejecting a 95% VaR model than a 99% VaR model.
D
Using a 99% VaR model will lower the probability of committing both Type I error
and Type II error.
Correct
Answer
A
Explanation
A is correct. The concept tested here is the understanding of the difference between
the VaR parameter for confidence (here, namely 95% vs. 99%) and the validation
procedure confidence level (namely 95%), and how they interact with one another.
Using a 95% VaR confidence level creates a narrower nonrejection region than
using a 99% VaR confidence level by allowing a greater number of exceptions to be
generated. This in turn increases the power of the backtesting process and makes
for a more reliable test than using a 99% confidence level.

 

[David Harper CFA FRM]

HI @PKuma9691 We've discussed this problematic question extensively. GARP seems to have revised it multiple times, but I think I generally concluded that it has problems in the wording. Put simply, it's GARP's fault if the PQ is not clear, and it ends up wasting people's time when they assume the solution is correctly specified (nevermind the new version of choice A is grammatically confusing). See https://forum.bionicturtle.com/threads/garp-2020-p2-53-and-garp-2019-p2-53.22374/post-75484 and https://forum.bionicturtle.com/thre...-backtest-significance-jorion.3604/post-59873