P1.T4.910. Barbells and bullets (Tuckman Ch.4)

[Nicole Seaman]

Learning objectives: Explain the process of calculating the effective duration and convexity of a portfolio of fixed income securities. Explain the impact of negative convexity on the hedging of fixed income securities. Construct a barbell portfolio to match the cost and duration of a given bullet investment, and explain the advantages and disadvantages of bullet versus barbell portfolios.

Questions:

910.1. The table below (which is a modified version of Tuckman's Table 4.3) displays the price of a 6 7/8 bond at various yield ("rate") levels: (Bruce Tuckman, Fixed Income Securities, 3rd Edition (Hoboken, NJ: John Wiley & Sons, 2011))

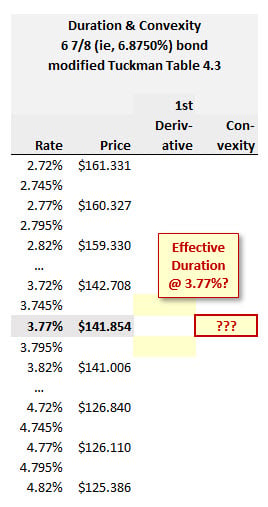
At a rate level of 3.77%, which of the following are nearest, respectively, to the bond's effective duration and convexity?

a. 7.7 years and ~89 years-squared
b. 9.5 years and ~113 years-squared
c. 12.0 years and ~169 years-squared
d. 15.3 years and ~250 years-squared


910.2. In the course of business on May 28, 2019, a market maker sells $200.0 million face amount of the option, TYU0C 120, when its DV01 is $0.03505. The market maker immediately seeks to put on a DV01 hedge (aka, to neutralize its DV01 exposure) with a long position in future contracts, TYU0, when its DV01 is 0.07442. Consequently, the market maker purchases about $94.2 million face amount of the futures contract: $200.0 * 0.03505/0.07442 = $94.2 million. In regard to the market maker's net position, which of the following statements is TRUE?

a. After a 50 basis point increase in rates, the market maker experiences a material loss
b. After a 50 basis point decrease in rates, the market maker experiences a material gain
c. If rates are highly volatile, the long futures position will outperform the option position
d. After a three basis point change in rates in either direction, the market maker experiences a material gain


910.3. On May 28, 2019, Robin the Portfolio Manager considers the purchase of $100.0 million face amount of the U.S. Treasury 2 3/8s (2.375%) due November 15, 2028, at a cost of $90,250,000. She refers to this as her "bullet" investment. After an analysis of the interest rate environment, she is comfortable with the pricing of the bond at a yield of 3.60% and with its duration of 8.32 years

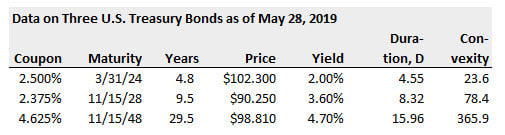
However, upon further inspection, Robin considers an alternative to the above-mentioned bullet investment in the 10-year 2 3/8s. Specifically, the alternative is a "barbell" investment in the shorter maturity 5-year 2 1/2s and the longer maturity 30-year 4 5/8s. The barbell would be constructed to have the same COST and DURATION as the bullet investment. Which of the following is nearest to the convexity of the alternative barbell portfolio?

a. 50.4 years^2
b. 78.4 years^2
c. 136.7 years^2
d. 305.9 years^2

Answers here:

• In forum

 

[Sahil1999]

Hi David,

Confused with a few things in 910.2,

The answer choices refer the increase, decrease and volatility of "rates". Which "rates" are we exactly talking about here, when looking at a position of short call options ? Since the position is in options, I assumed it to be the risk-free rate.

As per put call parity a higher risk-free rate will lead to an increase in the value of call option [Co + K*e^(-rf*t) = Po +So]
Since, the position taken by the market maker is short call (as given in the question), I assumed that the trader has already sold the calls for a lower price and now the value of the call option is high due to an increase of 50bps in the risk-free rate. Hence, the trader suffers a loss.

That's how I understood this. Can you please explain how is the DV01 hedge coming into picture here ?

I was not able to exactly understand the given solution.

 

[David Harper CFA FRM]

Hi @Sahil1999 Right, a more precise question should identify which interest "rate". You have a point. However, this question is closely based on Tuckman and (in my opinion) it is fair game: you've got to assume it's the same "rate" that informs the DV01s in the setup (i.e., probably yield as our DV01 is typically a yield-based DV01, but it could alternatively be a par-yield DV01!). Any DV01 by definition is based on an interest rate factor. We actually do not need to know which interest rate factor!

So, as explained in the source's thread at https://forum.bionicturtle.com/threads/p1-t4-910-barbells-and-bullets-tuckman-ch-4.22224/ this is really just a matter of (as I wrote there) ...

The market maker has two positions: writing (short) options hedged by purchased (long) futures; as the P/Y curve of futures is somewhat linear, the MM is short convexity like any option writer is short convexity.

The futures contract is (much more) linear while the option (as usual) has convexity (aka, gamma), so this is really about the fact that the DV01 hedge is only accurate locally and exposed to the short convexity (aka, short gamma) of the option. Thanks,