Questions:
322.1. Using the dataset from Stock & Watson (S&W), we used Excel's LINEST() function to regress student test scores (TestScore, the dependent regressand) against three independent variables: student teacher ratio (STR); percent of of english learners (EL_PCT); and percent qualifying for reduced-price lunch (MEAL_PCT). The multivariate regression results, which are also given by S&W 7.19, are displayed below:
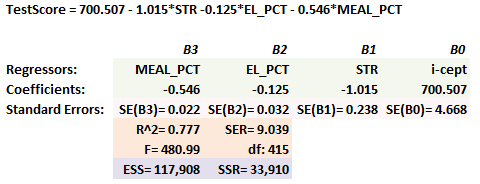
The dataset includes 419 observations. Each of the following is true about the regression model EXCEPT which is false?
a. Each of the single regression coefficients are individually significant with 95.0% confidence
b. The standard error of regression (SER) = SQRT[33,910/(419 - 3 - 1)]
c. The adjusted R^2 is less than the unadjusted R^2 of 0.777= 117,908/(117,908 + 33,910)
d. The atypical relationship between the F ratio and the R^2 suggests a hypothesis of (i.e., provide evidence for) omitted variable bias
322.2. The following regression model is from Stock & Watson's (S&W) "Growth" dataset. The model regresses annual growth in real Gross Domestic Product (GROWTH) against five independent regressors: real per capital GDP (RGDP); average share of trade in the economy (TRADE); average number of years of schooling of adult residents (SCHOOL); average annual number of revolutions or insurrections (REVOL); and average annual number of political assassinations (ASSASSIN):
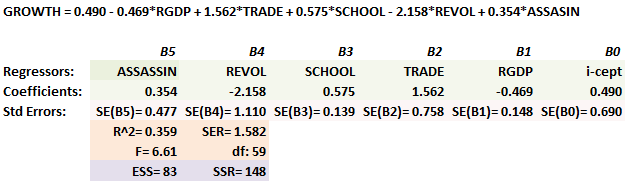
The dataset contains 65 countries (i.e., SSR df = 65 - 5 partial slope estimates - 1 intercept estimate) and the displayed R^2 of 0.359 is an unadjusted R^2 as suggested by ESS and SSR.Each of the following is true about this regression model EXCEPT which is false?
a. The partial effect of SCHOOL on GROWTH (the dependent variable) is positive and significant
b. A 95.0% confidence interval for the true value of SCHOOL is about 0.30 to 0.85
c. The correlation coefficient between GROWTH and the independent variables is about 0.60 = SQRT(0.359)
d. The adjusted R^2 = 0.305 = 1 - [(148/231)*(65-1)/(65-5-1)]
322.3. Each of the following statements is true about the classical linear regression model (CLRM) which uses the method of ordinary least squares (OLS) to estimate the coefficients in a multivariate regression EXCEPT which is false?
a. Omitted variable bias occurs if both (i) an omitted variable is a determinant of the dependent variable and (ii) at least one of the included independent variables (regressors) is correlated with the omitted variable
b. If we add an additional regressor and the adjusted R^2 increases, then this implies (i) the regressor is statistically significant, (ii) the regressor is a true cause of the dependent variable and (iii) there is no omitted variable bias
c. If the regression error is heteroskedastic, the OLS estimators are no longer "efficient" (they are linear and unbiased, but not BLUE); however, heteroskedasticity-robust standard errors are available and advisable
d. The CLRM OLS assumes no perfect multicollinearity (i.e., no exact collinearity between regressors), however imperfect does not necessarily prevent estimation of of the regression nor does it imply a logical problem with the choice of regressors
Answers:
322.1. Using the dataset from Stock & Watson (S&W), we used Excel's LINEST() function to regress student test scores (TestScore, the dependent regressand) against three independent variables: student teacher ratio (STR); percent of of english learners (EL_PCT); and percent qualifying for reduced-price lunch (MEAL_PCT). The multivariate regression results, which are also given by S&W 7.19, are displayed below:

The dataset includes 419 observations. Each of the following is true about the regression model EXCEPT which is false?
a. Each of the single regression coefficients are individually significant with 95.0% confidence
b. The standard error of regression (SER) = SQRT[33,910/(419 - 3 - 1)]
c. The adjusted R^2 is less than the unadjusted R^2 of 0.777= 117,908/(117,908 + 33,910)
d. The atypical relationship between the F ratio and the R^2 suggests a hypothesis of (i.e., provide evidence for) omitted variable bias
322.2. The following regression model is from Stock & Watson's (S&W) "Growth" dataset. The model regresses annual growth in real Gross Domestic Product (GROWTH) against five independent regressors: real per capital GDP (RGDP); average share of trade in the economy (TRADE); average number of years of schooling of adult residents (SCHOOL); average annual number of revolutions or insurrections (REVOL); and average annual number of political assassinations (ASSASSIN):

The dataset contains 65 countries (i.e., SSR df = 65 - 5 partial slope estimates - 1 intercept estimate) and the displayed R^2 of 0.359 is an unadjusted R^2 as suggested by ESS and SSR.Each of the following is true about this regression model EXCEPT which is false?
a. The partial effect of SCHOOL on GROWTH (the dependent variable) is positive and significant
b. A 95.0% confidence interval for the true value of SCHOOL is about 0.30 to 0.85
c. The correlation coefficient between GROWTH and the independent variables is about 0.60 = SQRT(0.359)
d. The adjusted R^2 = 0.305 = 1 - [(148/231)*(65-1)/(65-5-1)]
322.3. Each of the following statements is true about the classical linear regression model (CLRM) which uses the method of ordinary least squares (OLS) to estimate the coefficients in a multivariate regression EXCEPT which is false?
a. Omitted variable bias occurs if both (i) an omitted variable is a determinant of the dependent variable and (ii) at least one of the included independent variables (regressors) is correlated with the omitted variable
b. If we add an additional regressor and the adjusted R^2 increases, then this implies (i) the regressor is statistically significant, (ii) the regressor is a true cause of the dependent variable and (iii) there is no omitted variable bias
c. If the regression error is heteroskedastic, the OLS estimators are no longer "efficient" (they are linear and unbiased, but not BLUE); however, heteroskedasticity-robust standard errors are available and advisable
d. The CLRM OLS assumes no perfect multicollinearity (i.e., no exact collinearity between regressors), however imperfect does not necessarily prevent estimation of of the regression nor does it imply a logical problem with the choice of regressors
Answers:
