ps_ricky_son
Member
hi,
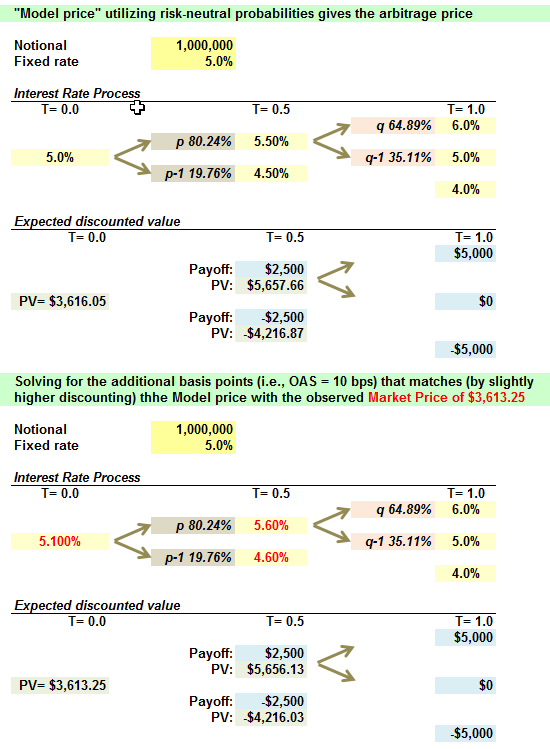
on p.28 of the notes P2.T5. (Bruce Tuckman, Fixed income securities), it says if the market price assumes to be $3,613.25, which is $2.8 less than the calculated model price of $3,616, the OAS turns out to be 10 basis points.
May I know how does this "10 basis points" come out? thanks for answering
on p.28 of the notes P2.T5. (Bruce Tuckman, Fixed income securities), it says if the market price assumes to be $3,613.25, which is $2.8 less than the calculated model price of $3,616, the OAS turns out to be 10 basis points.
May I know how does this "10 basis points" come out? thanks for answering