monsieuruzairo3
Member
Hi @David Harper CFA FRM CIPM & fellow Bionic Turtlers 
I came across a question on simple VaR calculation. The biggest challenge is interpreting the answers and calculation is quite simple
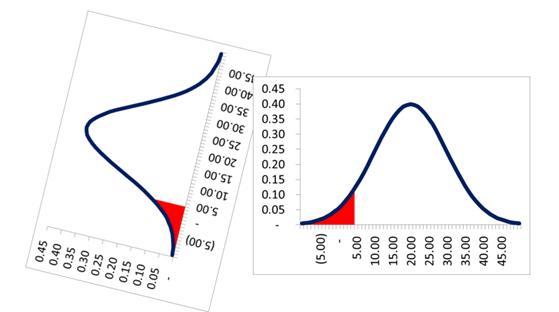
Q Mean 20 Mn$, volatility 10 Mn$. Normal VaR calculation at 5% significance
1) 5 % probability of losses of atleast 3.5 Mn$
2) 5% probability of earnings of atleast 3.5 Mn$
3) 95% probability of losses of atleast 3.5 Mn$
4) 95% probability of earnings of atleast 3.5 Mn$
My method
Var (5%) = -10 + 1.65*10 = -3.5 Mn $
Therefore loss is -3.5 Mn$ but since it is negative it is basically earnings of 3.5 Mn $
At 95% confidence this is the maximum earnings or at 5% this represents the minimum earning.
Therefore answer should be 2)5% probability of earnings of atleast 3.5 Mn$
However answer given is 4) 95% probability of earnings of atleast 3.5 Mn$
Am i missing a trick somewhere?
Many thanks in advance for the help
KR
Uzi

I came across a question on simple VaR calculation. The biggest challenge is interpreting the answers and calculation is quite simple
Q Mean 20 Mn$, volatility 10 Mn$. Normal VaR calculation at 5% significance
1) 5 % probability of losses of atleast 3.5 Mn$
2) 5% probability of earnings of atleast 3.5 Mn$
3) 95% probability of losses of atleast 3.5 Mn$
4) 95% probability of earnings of atleast 3.5 Mn$
My method
Var (5%) = -10 + 1.65*10 = -3.5 Mn $
Therefore loss is -3.5 Mn$ but since it is negative it is basically earnings of 3.5 Mn $
At 95% confidence this is the maximum earnings or at 5% this represents the minimum earning.
Therefore answer should be 2)5% probability of earnings of atleast 3.5 Mn$
However answer given is 4) 95% probability of earnings of atleast 3.5 Mn$
Am i missing a trick somewhere?
Many thanks in advance for the help
KR
Uzi