You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
jorion chapter 11 mapping var
- Thread starter Pflik
- Start date
-
- Tags
- mapping-var
angelbless
New Member
@David Harper CFA FRM.
Mr Harper, Im also having troubles with this chapter and the video. I could really use some help:
You said a theorethical spot rate curve was used for yield volatility (not the actual yield volatility of each bond right?), so:
1) In order to calculate Yield Volatility, I could use the treasury bonds volatility (with a specific maturity for each CF map right?) and the volatility of each one will be: a monthly volatility? annual volatility? or does it depends on the CF mapping?
2) How do I calculate yield VaR? or Price VaR?. I know they are related through the formula of PvaR= Durarion * Yield VaR, but in practice, I dont have any of those measures.
3)I recently read a Risk Metrics paper from JP Morgan, (I like Jorion´s method more than Risk Metrics), if you have read it, would you recommend me the methodoly for mapping CFs?
Thank you very much in advance.
Last edited:
Hi @ann123456 Yes you are correct that bond price returns VaR is the product of a change in yield and modified duration! However, Yield VaR is a change in yield. Let's take Jorion's own example, see below, for the 7-year term. The yield VaR is 0.484%. I don't think he anywere decomposes the yield VaR but Yield VaR = (Yield volatility) * (deviate); e.g., if yields are normal, then if the yield volatility is 1.0%, then the 95.0% yield VaR = 1.0% * 1.645 = 1.645%. So probably his 7-year yield VaR of 0.484% = 0.294% yield volatility * 1.645 = 0.484%. This is just a way of scaling volatility: "if the yield volatility is 294 basis points, then our worst expected change with 95% confidence is 484 basis points." In this way, this is a measure of yield change. Therefore, 7-year returns var = yield VaR * modified duration = 0.484% * 7/(1+6.07%) = 3.192 because the 0.484% itself is Δy*z(α), so we have returns VaR = Δy*z(a)*[Mac_duration/(1+y)] = 0.294%*1.645*(7/1.067) = 3.173%. I hope that helps!


Thankyou so much David !! That was really helpful !!!!Hi @ann123456 Yes you are correct that bond price returns VaR is the product of a change in yield and modified duration! However, Yield VaR is a change in yield. Let's take Jorion's own example, see below, for the 7-year term. The yield VaR is 0.484%. I don't think he anywere decomposes the yield VaR but Yield VaR = (Yield volatility) * (deviate); e.g., if yields are normal, then if the yield volatility is 1.0%, then the 95.0% yield VaR = 1.0% * 1.645 = 1.645%. So probably his 7-year yield VaR of 0.484% = 0.294% yield volatility * 1.645 = 0.484%. This is just a way of scaling volatility: "if the yield volatility is 294 basis points, then our worst expected change with 95% confidence is 484 basis points." In this way, this is a measure of yield change. Therefore, 7-year returns var = yield VaR * modified duration = 0.484% * 7/(1+6.07%) = 3.192 because the 0.484% itself is Δy*z(α), so we have returns VaR = Δy*z(a)*[Mac_duration/(1+y)] = 0.294%*1.645*(7/1.067) = 3.173%. I hope that helps!

Hi @Pflik,
Since VaR returns =|D*| x VaR(dY) we can solve for VaR yield
VaR change in yield =VaR(dP/P)/|D*|
Where D* is modified duration
Check out this video of David's
EDIT: I forgot to include that you can calculate Yield var by doing a historic simulation on the daily yield observations of the yield curve pertaining to that bond.
On another note (on this topic), I'm a bit confused by the mapping example table (below) in the study notes for Jorian chapter 11. I can't understand how each risk factor column is aggregated.
corinne.lieberman21
Member
Hi David,
Hi David, I’m not sure if I’m missing something but how do we calculate the 7 year yield var itself? Also, are we always supposed to assume 95% on these questions? Conf level is never actually specified in the videos or notes.Hi @ann123456 Yes you are correct that bond price returns VaR is the product of a change in yield and modified duration! However, Yield VaR is a change in yield. Let's take Jorion's own example, see below, for the 7-year term. The yield VaR is 0.484%. I don't think he anywere decomposes the yield VaR but Yield VaR = (Yield volatility) * (deviate); e.g., if yields are normal, then if the yield volatility is 1.0%, then the 95.0% yield VaR = 1.0% * 1.645 = 1.645%. So probably his 7-year yield VaR of 0.484% = 0.294% yield volatility * 1.645 = 0.484%. This is just a way of scaling volatility: "if the yield volatility is 294 basis points, then our worst expected change with 95% confidence is 484 basis points." In this way, this is a measure of yield change. Therefore, 7-year returns var = yield VaR * modified duration = 0.484% * 7/(1+6.07%) = 3.192 because the 0.484% itself is Δy*z(α), so we have returns VaR = Δy*z(a)*[Mac_duration/(1+y)] = 0.294%*1.645*(7/1.067) = 3.173%. I hope that helps!

Hi @corinne.lieberman21 I did not realize the confidence level is not explicitly stated, I apologize and have noted this for the next versions. You are correct: the confidence level must be explicitly stated. Re: "Also, are we always supposed to assume 95% on these questions?" No, because 99.0% is also common, you cannot know the confidence level. What happened here is simply that I am following Jorion who is assuming 95.0% confidence throughout the entire example (case study).
Further, we do need to be given the yield volatility. To retrieve a yield VaR, we need to be given the yield volatility and the confidence level; e.g., 1.0% yield volatility * 1.645 = 1.645% yield VaR if the confidence is 95.0%; 1.0% yield volatility * 2.33 = 2.33% yield VaR if the confidence is 99.0%. In fact, we should even be given that the "yields are normally distributed with volatility of X%" in order to know that 95.0% corresponds to 1.645.
So in fact, in order to get (eg) a yield VaR of 1.645%, there are three assumptions we need to be explicitly told: yield volatility of 1.0%; normally distributed yields; and the VaR confidence level (because only the normal has a 1.645 deviate at 95.0%). Thank you,
Further, we do need to be given the yield volatility. To retrieve a yield VaR, we need to be given the yield volatility and the confidence level; e.g., 1.0% yield volatility * 1.645 = 1.645% yield VaR if the confidence is 95.0%; 1.0% yield volatility * 2.33 = 2.33% yield VaR if the confidence is 99.0%. In fact, we should even be given that the "yields are normally distributed with volatility of X%" in order to know that 95.0% corresponds to 1.645.
So in fact, in order to get (eg) a yield VaR of 1.645%, there are three assumptions we need to be explicitly told: yield volatility of 1.0%; normally distributed yields; and the VaR confidence level (because only the normal has a 1.645 deviate at 95.0%). Thank you,
@wojtek See Jorion's explanation below. if we are long (purchase) the 6-month bill, the purchase is treated a cash outflow; if we sell (short) the 12-month bill, we receive cash and it's treated as an inflow. I think the important thing for mapping is they are different: i don't think it matters greatly (it may not matter at all!) if we instead map a short 6 × 12 FRA with a positive CF for shorting the 6-month plus a negative CF for purchase of 12-month bill. Thanks,
"For instance, suppose that you sold a 6 × 12 FRA on $100 million. This is equivalent to borrowing $100 million for 6 months and investing the proceeds for 12 months. When the FRA expires in 6 months, assume that the prevailing 6-month spot rate is higher than the locked-in forward rate. The seller then pays the buyer the difference between the spot and forward rates applied to the principal. In effect, this payment offsets the higher return that the investor otherwise would receive, thus guaranteeing a return equal to the forward rate. Therefore, an FRA can be decomposed into two zero-coupon building blocks.
Long 6 × 12 FRA = long 6-month bill + short 12-month bill" -- Philippe Jorion. Value at Risk, 3rd Ed.: The New Benchmark for Managing Financial Risk (pp. 294-295). Kindle Edition.
David, great thanks for your answer. I like entirely understand what I am reading. I have read carefully this chapter and the passage you cited and I think that the table presented in Jorion’s chapter for FRA concerns short FRA (negative CF in 6 months (180 days), positive CF in 12 months (360 days)). Yes, you are right that in mapping FRA it does not matter whether we calculate short or long FRA because signs are different but PV(CF) are the same. I also agree that long 6M bill (purchase) is outflow (-) and short (sell) 12 M bill is inflow(+) when open. But we are concerned about what is happening in 6M and 12M, not today. Today both CF cancel each other. If (as in Jorion‘s chapter) we have (-) in 6M and (+) in 12M it means, I think, that we pay (close short) in 6M and receive (close long) in 12 M. So it should be:@wojtek See Jorion's explanation below. if we are long (purchase) the 6-month bill, the purchase is treated a cash outflow; if we sell (short) the 12-month bill, we receive cash and it's treated as an inflow. I think the important thing for mapping is they are different: i don't think it matters greatly (it may not matter at all!) if we instead map a short 6 × 12 FRA with a positive CF for shorting the 6-month plus a negative CF for purchase of 12-month bill. Thanks,
Short 6x12 FRA= short 6M bill + long 12M bill
Is my reasoning right?
Hi @wojtek Yes, I agree with "Short 6x12 FRA= short 6M bill + long 12M bill" as it is the mirror image to Jorion's "Long 6×12 FRA = long 6-month bill + short 12-month bill". Below is a copy of his Table 11-9. My interpretation is that this maps a Short 6x12 FRA because there is a negative PV of Flows in the first row: -$100.00 mm notional /(1+ 5.6250%/2) = -$97.2644 or -$97.264; this must be the amount borrowed! By deduction, notice that if we borrowed the notional for 360 days, then we'd borrow only $100.00/(1+ 5.8125%/2)^2 = $94.431; but this is not the amount shown. Rather, the amount borrowed is the same amount invested ($97.264). Therefore, this Table 11-9, by deduction must be illustrating: short (borrow) $100.00 for six months and invest (long) the same amount for one year. (The negative is because these are PVs of future values: in six months the $100.00 must be repaid which is an outflow; in one year, the investment will be returned, which is a positive inflow). Therefore, it maps the Short 6x12 FRA. Of course, the point of the mapping is that the present value of the FRA will match the value of the mapped portfolio because this portfolio is effectively a bet on the six-month forward rate, F(0.5, 1.0). I hope that's helpful, thank you!


Hi, David (@David Harper CFA FRM )
Sorry to disturb you, I understand that you are busy with updating the material. However, while studying, I found myself having trouble understanding why the PV of the cash flows are all the same number. For example, the fx forward example in the study note:

I understood that -125.93 = -130.12*0.967769 = Future Cashflow($)/(1+USDRate). But for the long EUR bill, I'm quite sure the calculation logic. I suppose it's calculated by
-125.93 = 100*0.977699*1.2877 = Future Cashflow(Euro)/(1+EURRate)*FX(USD/EUR)
is this the right way to think about it?
Please let me know your thought.
Thank you!
Sorry to disturb you, I understand that you are busy with updating the material. However, while studying, I found myself having trouble understanding why the PV of the cash flows are all the same number. For example, the fx forward example in the study note:
I understood that -125.93 = -130.12*0.967769 = Future Cashflow($)/(1+USDRate). But for the long EUR bill, I'm quite sure the calculation logic. I suppose it's calculated by
-125.93 = 100*0.977699*1.2877 = Future Cashflow(Euro)/(1+EURRate)*FX(USD/EUR)
is this the right way to think about it?
Please let me know your thought.
Thank you!
Hi @txiong You know what, I think I miscalculated those mappings (and I didn't notice because my result is so near to Jorion's that I assumed rounding). As Jorion explains in 11.3, the mapping follows the valuation of the forward contract:
f = S*exp(-yt) - K*(exp-rT); except he discounts discretely. So here we have:
f = ($1.2877 * $100.00) * 1/(1 + 2.2810%) - ($1.3013 * $100.00) * 1/(1+3.3304%) = $125.898 - $125.934 ~= 0
where presumably the difference from zero is the compounding frequency, so that if i change the discounting to continuous then I get:
f = ($1.2877 * $100.00) * exp(-2.2810%) - ($1.3013 * $100.00) * exp(-3.3304%) = $125.866 - $125.866 = 0. Yay!
actually, i see now my mistake included to infer the the forward rate continuously, whereas Jorion's EUR forward is given by
$1.2877 * (1 + 3.3304%) / (1 + 2.2810%) = $1.3009 (versus the 1.3013 I am showing). Then I can match him with
f = S*df(1.0) - K*df(1.0)
f = ($1.2877 * $100.00) * 1/(1+2.2810%) - ($1.3009 * $100.00) * 1/(1+3.3304%) = 125.898 - 125.898 = 0; it must equal zero because the forward rate is solved for with the spot rates; it's internally consistent.
Thanks for helping me spot my calculation error, I hope this makes sense, I'll incorporate into the next note revision ...
f = S*exp(-yt) - K*(exp-rT); except he discounts discretely. So here we have:
f = ($1.2877 * $100.00) * 1/(1 + 2.2810%) - ($1.3013 * $100.00) * 1/(1+3.3304%) = $125.898 - $125.934 ~= 0
where presumably the difference from zero is the compounding frequency, so that if i change the discounting to continuous then I get:
f = ($1.2877 * $100.00) * exp(-2.2810%) - ($1.3013 * $100.00) * exp(-3.3304%) = $125.866 - $125.866 = 0. Yay!
actually, i see now my mistake included to infer the the forward rate continuously, whereas Jorion's EUR forward is given by
$1.2877 * (1 + 3.3304%) / (1 + 2.2810%) = $1.3009 (versus the 1.3013 I am showing). Then I can match him with
f = S*df(1.0) - K*df(1.0)
f = ($1.2877 * $100.00) * 1/(1+2.2810%) - ($1.3009 * $100.00) * 1/(1+3.3304%) = 125.898 - 125.898 = 0; it must equal zero because the forward rate is solved for with the spot rates; it's internally consistent.
Thanks for helping me spot my calculation error, I hope this makes sense, I'll incorporate into the next note revision ...
Last edited:
Hi, David (@David Harper CFA FRM )
Thank you for the interpretation. This is much clearer now. Glad I can provide help.
Frank
Thank you for the interpretation. This is much clearer now. Glad I can provide help.
Frank
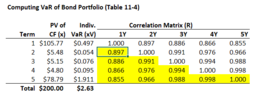
good morning,
sorry for the basic question but would you share some light of the calculation behind the 0.897, for example? I've been trying for a while to replicate, but it was no succeed.
thanks!
View attachment 3936
It is an correlation matrix as input. it is more like an assumption. No calculation behind them.
They use it as input to derive the diversified VaR.
@jchun8523 Yes @yLam4028 is correct: those pairwise correlations are purely assumptions (you would not be able to derive or replicate them!). They are colored in YELLOW which in our XLS does connote input assumptions. Thanks,
Similar threads
- Replies
- 0
- Views
- 303
- Replies
- 0
- Views
- 1K
- Replies
- 0
- Views
- 478