Steve Jobs
Active Member
Hi,
In FRM1, it was S+c = Ke + p
In FRM2, I found 2 practice questions:
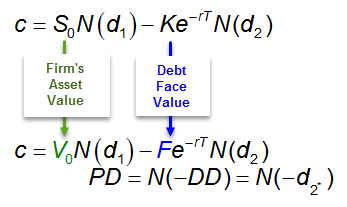
-In first question, the question gives the V for Value of firm, F for Face value debt, S for value of equity and then asking for p.
In the provided answer, the c is substituted with value of equity and p is calculated.
-In the second question, the value of c is given and then the question is asking for value of equity.
To calculate the value of equity, this formula used E=A-Dt which is understandable but not consistent with the answer provided for the first question; I though according to the first question c = value of equity.
Do you see the inconsistency?
In FRM1, it was S+c = Ke + p
In FRM2, I found 2 practice questions:
-In first question, the question gives the V for Value of firm, F for Face value debt, S for value of equity and then asking for p.
In the provided answer, the c is substituted with value of equity and p is calculated.
-In the second question, the value of c is given and then the question is asking for value of equity.
To calculate the value of equity, this formula used E=A-Dt which is understandable but not consistent with the answer provided for the first question; I though according to the first question c = value of equity.
Do you see the inconsistency?


 ).
).