Unusualskill
Member
Hi,
I have question for Hull, Chapter 7, Swaps. I am quite confused about calculating the value of the floating rate bond.
Referring to this example:
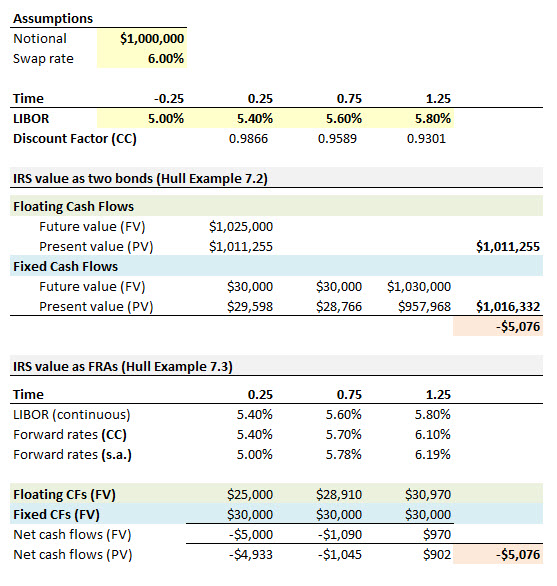
Consider a $1 million notional swap that pays a floating rate based on 6-month LIBOR
and receives a 6% fixed rate semiannually. The swap has a remaining life o f 15 months
with pay dates at 3, 9, and 13 months. Spot LIBOR rates are as follows: 3 months at
5.4%; 9 months at 5.6%; and 15 months at 5.8%. The LIBOR at the last payment
date was 5.0%. Calculate the value of the swap to the fixed-rate receiver using the bond
methodology.
(i)What is the difference between Spot LIBOR rates above and the LIBOR at the last payment date?
(ii)Bfloating =[ $1,000,000 + ($ l,000,0 0 0 x 0.05/2)] x e-(0.054 x 0.25) = $ 1,011,255
Why only use 5%?
Any good explanations on these two topics?
(i)Calculate the value of a plain vanilla interest rate swap based on two simultaneous bond positions.
(ii)Calculate the value of a plain vanilla interest rate swap from a sequence of forward rate agreements (FRAs).
Thank you!
I have question for Hull, Chapter 7, Swaps. I am quite confused about calculating the value of the floating rate bond.
Referring to this example:
Consider a $1 million notional swap that pays a floating rate based on 6-month LIBOR
and receives a 6% fixed rate semiannually. The swap has a remaining life o f 15 months
with pay dates at 3, 9, and 13 months. Spot LIBOR rates are as follows: 3 months at
5.4%; 9 months at 5.6%; and 15 months at 5.8%. The LIBOR at the last payment
date was 5.0%. Calculate the value of the swap to the fixed-rate receiver using the bond
methodology.
(i)What is the difference between Spot LIBOR rates above and the LIBOR at the last payment date?
(ii)Bfloating =[ $1,000,000 + ($ l,000,0 0 0 x 0.05/2)] x e-(0.054 x 0.25) = $ 1,011,255
Why only use 5%?
Any good explanations on these two topics?
(i)Calculate the value of a plain vanilla interest rate swap based on two simultaneous bond positions.
(ii)Calculate the value of a plain vanilla interest rate swap from a sequence of forward rate agreements (FRAs).
Thank you!