[email protected]
New Member
Hi David,
I hope you are well.
On an interview I was asked what is the sensitivity of the Sharpe's ratio to the volatility,
The interviewer told it is almost zero...
Could you give a hint please?
Many thanks,
Indira
I hope you are well.
On an interview I was asked what is the sensitivity of the Sharpe's ratio to the volatility,
The interviewer told it is almost zero...
Could you give a hint please?
Many thanks,
Indira

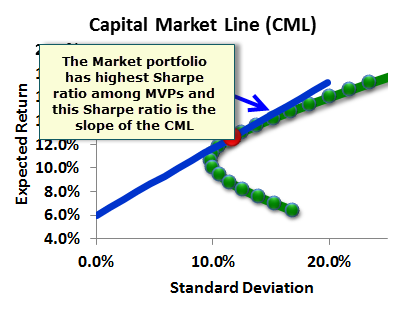
 ) in his first few lines, the Sharpe ratio of a (perfectly) diversified portfolio is equal to the Sharpe ratio of the market portfolio. This is a key feature of the capital market line (CML): unlike the SML, all points (portfolios) on the CML, which includes the Market Portfolio, are efficient with identical Sharpe ratios which correspond to the slope of the CML:
) in his first few lines, the Sharpe ratio of a (perfectly) diversified portfolio is equal to the Sharpe ratio of the market portfolio. This is a key feature of the capital market line (CML): unlike the SML, all points (portfolios) on the CML, which includes the Market Portfolio, are efficient with identical Sharpe ratios which correspond to the slope of the CML: