Hi @David Harper CFA FRM
Apologies for the basic question, but what's the intuition behind the Modified Duration calculation in cell D30 of:
https://learn.bionicturtle.com/FRM/...ets/R36-P2-T5-Jorion-mapping-backtest-v3.xlsx
Using the definition below for Macaulay Duration I was able to replicate the values in the orange highlighted block in the bottom right of my screenshot below, but your way is much faster
https://www.investopedia.com/terms/m/macaulayduration.asp
Screenshot of your file with my calculations added:
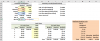
However I'm not going to remember your formula easily if I don't understand the intuition behind it.
Thanks!
Karim
Apologies for the basic question, but what's the intuition behind the Modified Duration calculation in cell D30 of:
https://learn.bionicturtle.com/FRM/...ets/R36-P2-T5-Jorion-mapping-backtest-v3.xlsx
Using the definition below for Macaulay Duration I was able to replicate the values in the orange highlighted block in the bottom right of my screenshot below, but your way is much faster

https://www.investopedia.com/terms/m/macaulayduration.asp
Screenshot of your file with my calculations added:
However I'm not going to remember your formula easily if I don't understand the intuition behind it.
Thanks!
Karim

