Shazam023
New Member
i just gone through Vasicek model for "Worst Case Default Rate"
and the formula says:-
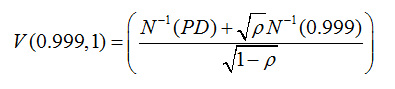
in most of the cases X= 99.1% and N= 1 year.
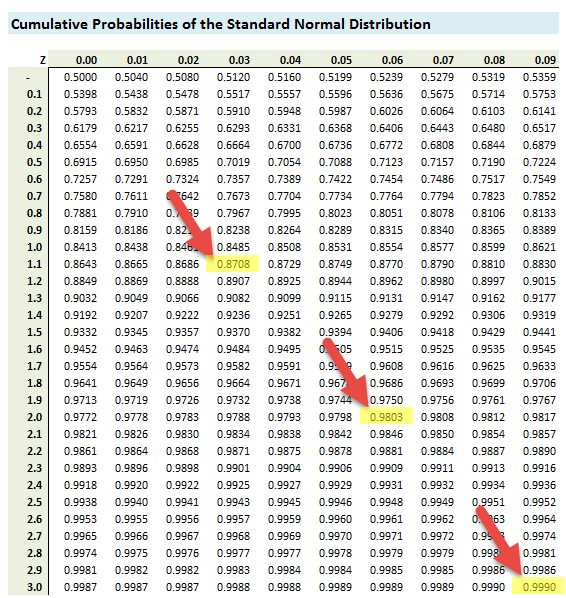
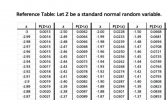
the issue is i'm not able to get the of N^-1 ?? how to solve this??
Ques:
Suppose that a bank has a total of $100 million of retail exposures of varying sizes with each exposure being small in relation to
the total exposure. The one-year probability of default for each loan is 2% and the loss given default for each loan is 40%. The
copula correlation parameter, is estimated as 0.1.
Answer: WCDR (0.999,1)= 0.128
i'm not getting this 0128
please help
and the formula says:-
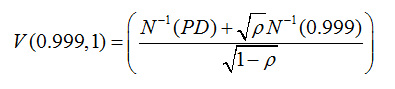
in most of the cases X= 99.1% and N= 1 year.
the issue is i'm not able to get the of N^-1 ?? how to solve this??
Ques:
Suppose that a bank has a total of $100 million of retail exposures of varying sizes with each exposure being small in relation to
the total exposure. The one-year probability of default for each loan is 2% and the loss given default for each loan is 40%. The
copula correlation parameter, is estimated as 0.1.
Answer: WCDR (0.999,1)= 0.128
i'm not getting this 0128
please help