Hi David,
I am a little confused about the three terms above though I know how to calculate them.
(1) What is Unexpected Loss (UL)?
Let L, EL and UL denote Loss, Expected Loss and Unexpected Loss respectively.
UL can be defined as the standard deviation of EL (according to Kaplan).
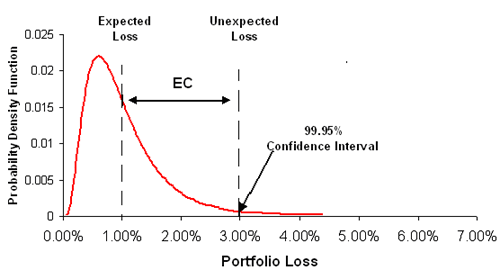
But looking at your (very nice) chart in the following post: http://forum.bionicturtle.com/viewthread/1734/
UL = EL + 1 x STDEV( L ).
How does that fit together?
(2) What is Econimc Capital (EC) ?
I find two contradicting statements in Kaplan:
a) EC = UL - EL ( only losses in excess of EL )
b) EC = UL
Can you help me out?
Kind regards,
Roman.
I am a little confused about the three terms above though I know how to calculate them.
(1) What is Unexpected Loss (UL)?
Let L, EL and UL denote Loss, Expected Loss and Unexpected Loss respectively.
UL can be defined as the standard deviation of EL (according to Kaplan).
But looking at your (very nice) chart in the following post: http://forum.bionicturtle.com/viewthread/1734/
UL = EL + 1 x STDEV( L ).
How does that fit together?
(2) What is Econimc Capital (EC) ?
I find two contradicting statements in Kaplan:
a) EC = UL - EL ( only losses in excess of EL )
b) EC = UL
Can you help me out?
Kind regards,
Roman.