afterworkguinness
Active Member
Sorry to be that guy who keeps posting questions, this really is by far the best resource out there.
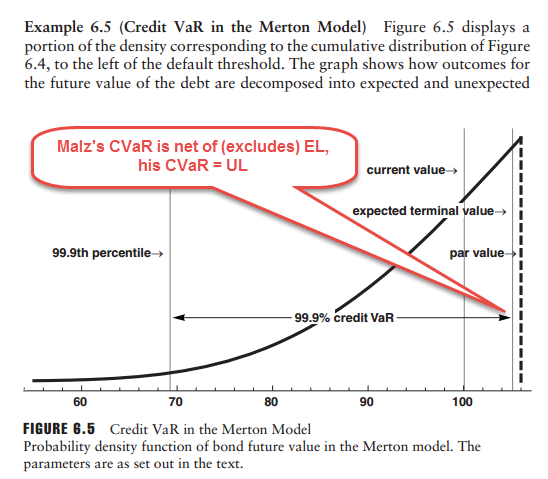
The answer to practice question 305.3 for Malz says the following statement is true:
CVaR (alpha) = Unexpected loss (alpha), where alpha is a significance or confidence level
Q: if CVaR is Expected loss - Unexpected loss, how is this true ?
(can't view/post in the thread for this question set as my BT package expired)
The answer to practice question 305.3 for Malz says the following statement is true:
CVaR (alpha) = Unexpected loss (alpha), where alpha is a significance or confidence level
Q: if CVaR is Expected loss - Unexpected loss, how is this true ?
(can't view/post in the thread for this question set as my BT package expired)