You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Eurodollar Convexity ADjustment
- Thread starter skoh
- Start date
Backwardation
Member
the foward rate should be lower than the future rate for IR products, because of the disadvantageous margin system of futures
hi,
convexity= rate of change of duration w.r.t yield y, its a double derivative
D1=V- - V0/V0*chg y ..duration is percent change in price wrt change in % yield
D2= V0- V+/V0*chg y
convexity= D1-D2/2*chg y
convexity=[V- - V0/chg y]-[ V0- V+/chg y]/2V0**chg y
convexity=[V- - V0]-[ V0- V+]/2V0**chg y^2
convexity=[V- + V+ - 2V0]/2V0**chg y^2
thanks
convexity= rate of change of duration w.r.t yield y, its a double derivative
D1=V- - V0/V0*chg y ..duration is percent change in price wrt change in % yield
D2= V0- V+/V0*chg y
convexity= D1-D2/2*chg y
convexity=[V- - V0/chg y]-[ V0- V+/chg y]/2V0**chg y
convexity=[V- - V0]-[ V0- V+]/2V0**chg y^2
convexity=[V- + V+ - 2V0]/2V0**chg y^2
thanks
Praveen_India
Member
Hi David/Forum,
Reference:R12.P1.T3.HULL_V3
Convexity adjustment for ED Futures:
Futures rate (ACT/360) 5.000% = 100 – 95 price
1.250% Per 90 days
5.038% = LN (1.0125)*365/90;
Annualised Libor rate is 5%(compounded quarterly). When we want to convert it to a rate compounded continuously we use the formula:
Rc=m*LN(1+(Rm/m))
So, Rc=4*LN(1+(.05/4))= 4.969% but as per the above calculation it is 5.038%, which is greater than the quarterly compounded rate of 5%.
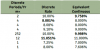
As seen above continuous compounded rate is always lesser than non continuously compounded rate.
Kindly help me understand the logic here.
Thanks,
Praveen
Reference:R12.P1.T3.HULL_V3
Convexity adjustment for ED Futures:
Futures rate (ACT/360) 5.000% = 100 – 95 price
1.250% Per 90 days
5.038% = LN (1.0125)*365/90;
Annualised Libor rate is 5%(compounded quarterly). When we want to convert it to a rate compounded continuously we use the formula:
Rc=m*LN(1+(Rm/m))
So, Rc=4*LN(1+(.05/4))= 4.969% but as per the above calculation it is 5.038%, which is greater than the quarterly compounded rate of 5%.
As seen above continuous compounded rate is always lesser than non continuously compounded rate.
Kindly help me understand the logic here.
Thanks,
Praveen
Attachments
Hi
The formula Rc=m*LN(1+(Rm/m)) requires that m(both values one below Rm and other which is multipling with log factor) is same i mean in expression *5.038% = LN (1.0125)*365/90;* m assumes two different values 4(360/90) and 365/90 so the result 5.038% is not consistent with result that continous compiunded rate is always less than discrete rate.only when values of m are equal on then a less continous rate results. The violation of variable m equality leds to the downfall of the formula Rc=m*LN(1+(Rm/m)).
Please see that convention actual/365 make difference.
Thanks
The formula Rc=m*LN(1+(Rm/m)) requires that m(both values one below Rm and other which is multipling with log factor) is same i mean in expression *5.038% = LN (1.0125)*365/90;* m assumes two different values 4(360/90) and 365/90 so the result 5.038% is not consistent with result that continous compiunded rate is always less than discrete rate.only when values of m are equal on then a less continous rate results. The violation of variable m equality leds to the downfall of the formula Rc=m*LN(1+(Rm/m)).
Please see that convention actual/365 make difference.
Thanks
Last edited:
Praveen_India
Member
Hi Shakti,
Right, i got your explanation about the difference in the two expressions. However, logically speaking continuously compounded rate should be less than its equivalent non continuously compounded rate, whatever formula is used. but here its not the case.
And as for my 1st doubt, i have not understood the formula in bold in first place. We have annual rate of 5%, but first we are converting it to quarterly, then again calculating annual continuous compound rate. cant we use the formula (Rc=m*LN(1+(Rm/m))) directly. Please can you explain the formula in bold and when to use it.
Futures rate (ACT/360) 5.000% = 100 – 95 price
1.250% Per 90 days
5.038% = LN (1.0125)*365/90;
Thanks,
Praveen
Right, i got your explanation about the difference in the two expressions. However, logically speaking continuously compounded rate should be less than its equivalent non continuously compounded rate, whatever formula is used. but here its not the case.
And as for my 1st doubt, i have not understood the formula in bold in first place. We have annual rate of 5%, but first we are converting it to quarterly, then again calculating annual continuous compound rate. cant we use the formula (Rc=m*LN(1+(Rm/m))) directly. Please can you explain the formula in bold and when to use it.
Futures rate (ACT/360) 5.000% = 100 – 95 price
1.250% Per 90 days
5.038% = LN (1.0125)*365/90;
Thanks,
Praveen
Hi,
Raise both sides of Equation with base as e we get,
e^ 5.038% =e^(365/90* LN (1.0125))
e^ 5.038% =e^(LN (1.0125)^365/90))
e^ 5.038% =(1.0125)^365/90 here we are conpounding discrete rate if 5% over 365 days rather than 360 days.for continous rate 1 yr is 360 days(used 5%/4 i.e. 90/360 instead of 90/365 if it was used we would have lower cont. Rate) in order to account for extra 5 days we use a higher continous rate.
For holding relation cont.ratr<=discrete rate the period of discrete conpounding shall be sams period of cont. Conpounding 360 daya in this case,however here its not the case so disc. Compounding periid of 365 days is different than cont. Comp period of 360 d.
See the difference is that discrete rate is compounded over 365 days rather than 360 days.Discrete rate is given as 1.25% over 90 days. .
Thanks
Raise both sides of Equation with base as e we get,
e^ 5.038% =e^(365/90* LN (1.0125))
e^ 5.038% =e^(LN (1.0125)^365/90))
e^ 5.038% =(1.0125)^365/90 here we are conpounding discrete rate if 5% over 365 days rather than 360 days.for continous rate 1 yr is 360 days(used 5%/4 i.e. 90/360 instead of 90/365 if it was used we would have lower cont. Rate) in order to account for extra 5 days we use a higher continous rate.
For holding relation cont.ratr<=discrete rate the period of discrete conpounding shall be sams period of cont. Conpounding 360 daya in this case,however here its not the case so disc. Compounding periid of 365 days is different than cont. Comp period of 360 d.
See the difference is that discrete rate is compounded over 365 days rather than 360 days.Discrete rate is given as 1.25% over 90 days. .
Thanks
Last edited:
Thank you @ShaktiRathore, indeed!
@Praveen_India The confusion is because the formula, as Shakti shows, is performing two operations (I am following Hull here, it has caused much confusion!). We can break it up:
@Praveen_India The confusion is because the formula, as Shakti shows, is performing two operations (I am following Hull here, it has caused much confusion!). We can break it up:
- 4.6969% = 4*LN(1+5%/4); ie, satisfies the condition to which you refer! ... but there is an additional operation:
- 4.6969% * 365/360 = 5.038% performs a day count adjustment. I hope that helps!
Praveen_India
Member
Thanks a lot David and Shakti for the explanation.
One more question is are we doing this day count conversion because Euro Dollars use ACT/360 and the Convexity adjustment model: Forward=Future-1/2* variance* t1*t2 is based on the assumption ACT/365?
Thanks,
Praveen
One more question is are we doing this day count conversion because Euro Dollars use ACT/360 and the Convexity adjustment model: Forward=Future-1/2* variance* t1*t2 is based on the assumption ACT/365?
Thanks,
Praveen
Hi @Praveen_India
It's a good question. What is certain is that Eurodollar futures are quoted with quarterly compounding and an actual/360 day count convention. It's a contractual spec: the ED contract uses LIBOR (http://www.cmegroup.com/trading/interest-rates/stir/eurodollar_contract_specifications.html) and the LIBOR, in trun, assumes quarterly actual/360 (http://wiki.treasurers.org/wiki/Day_count_conventions).
The Ho-Lee adjustment naturally assumes continuous compounding (like many theoretical computations that utilize calculus), but I am not entirely certain, to be candid, whether the 365/360 adjustment is necessary. Maybe @ShaktiRathore knows? But, clearly they need to be apples-to-apples such I simply infer that the Ho-Lee adjustment naturally assumes 365 days; or, the calculation simply wants to be on "actual days."
Here is my best resource on the topic, Chapter 6 of Interest Rate Risk Modeling (Nawalkha et al), they go into greater detail on the convexity adjustment that Hull briefly discusses: https://www.dropbox.com/s/joo6fyq5r...Risk Modeling-Ch6-Hedging-IR-futures.pdf?dl=0
I hope that helps, David
It's a good question. What is certain is that Eurodollar futures are quoted with quarterly compounding and an actual/360 day count convention. It's a contractual spec: the ED contract uses LIBOR (http://www.cmegroup.com/trading/interest-rates/stir/eurodollar_contract_specifications.html) and the LIBOR, in trun, assumes quarterly actual/360 (http://wiki.treasurers.org/wiki/Day_count_conventions).
The Ho-Lee adjustment naturally assumes continuous compounding (like many theoretical computations that utilize calculus), but I am not entirely certain, to be candid, whether the 365/360 adjustment is necessary. Maybe @ShaktiRathore knows? But, clearly they need to be apples-to-apples such I simply infer that the Ho-Lee adjustment naturally assumes 365 days; or, the calculation simply wants to be on "actual days."
Here is my best resource on the topic, Chapter 6 of Interest Rate Risk Modeling (Nawalkha et al), they go into greater detail on the convexity adjustment that Hull briefly discusses: https://www.dropbox.com/s/joo6fyq5r...Risk Modeling-Ch6-Hedging-IR-futures.pdf?dl=0
I hope that helps, David
Praveen_India
Member
Thanks for the explanation David.
Similar threads
- Replies
- 0
- Views
- 245
- Replies
- 2
- Views
- 735
- Replies
- 0
- Views
- 1K
- Replies
- 0
- Views
- 600
- Replies
- 0
- Views
- 485
