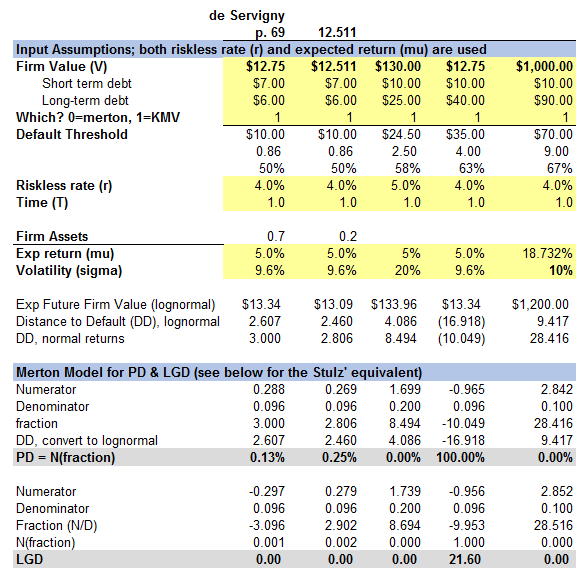
I am reading de Servigny's Default Risk Quantitative Methodologies chapter from the GARP printed textbooks.
Page 69 references the Black-Scholes pricing model for the value of a firm's equity under the Merton model.
Interestingly, the formula does not reference d1 yet the expression is immediately followed by a "where d1 = ..." statement.

Does any know if this is a careless GARP error or does the actual de Servigny text also have the same error?
Obviously, we recognize d1 from the Black-Scholes model.
Best,
Brian
Page 69 references the Black-Scholes pricing model for the value of a firm's equity under the Merton model.
Interestingly, the formula does not reference d1 yet the expression is immediately followed by a "where d1 = ..." statement.
Does any know if this is a careless GARP error or does the actual de Servigny text also have the same error?
Obviously, we recognize d1 from the Black-Scholes model.
Best,
Brian


 He could have indicated that the base was e.
He could have indicated that the base was e.