kevolution
Member
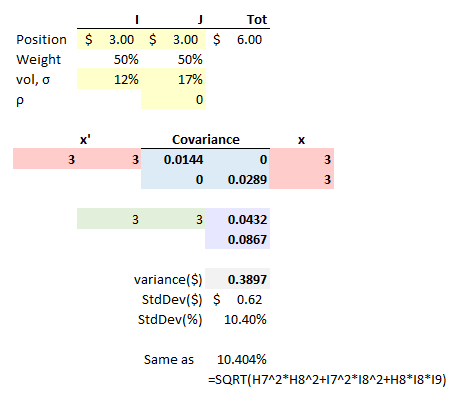
I was looking at this specific 2-asset portfolio example and noticed that BT uses the matrix formula to get the variance of P.
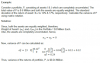
What I'm confused about is why do you not use the variance formula: variance = X1^2*stddev(asset1)^2 + X2^2*stddev(asset2)^2 + 2*X1*X2*stddev(asset1)*stddev(asset2)*correlation
where X1 and X2 are the weights (in this case 0.5 and 0.5). The correlation part of the summation gets canceled out since it's 0 for this problem.
I get a different answer when using the above formula vs. the covariance matrix method. I got variance = 0.0108
Please tell me what I'm doing wrong. Thanks!
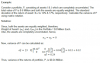
What I'm confused about is why do you not use the variance formula: variance = X1^2*stddev(asset1)^2 + X2^2*stddev(asset2)^2 + 2*X1*X2*stddev(asset1)*stddev(asset2)*correlation
where X1 and X2 are the weights (in this case 0.5 and 0.5). The correlation part of the summation gets canceled out since it's 0 for this problem.
I get a different answer when using the above formula vs. the covariance matrix method. I got variance = 0.0108
Please tell me what I'm doing wrong. Thanks!