Correlation in CDS

[Sunil Natarajan]

Hi David,
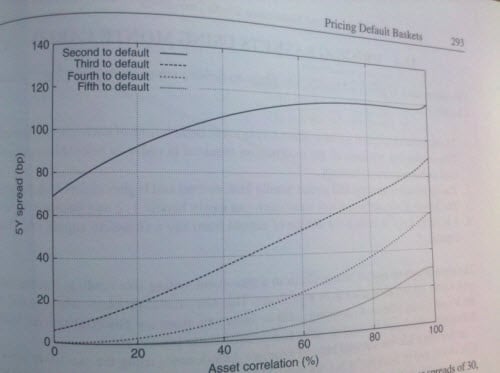
I have a small doubt about correlation in Nth default swap.In chapter 22 of Jorion (page 504) he mentions that type of protection depends upon correlation between credit events(is he referring credit events to default).Lower the correlation more expensive the swap(higher cost of protection) and vice versa. Does this imply basket swap premium is higher with low correlation of default? He then mentions in the next para that when N is large the higher default correlation would lead to higher cost of protection. It seems contradicting to me.
I have a doubt please correct me if Iam wrong CDS is more of an option as compared to it being a swap. The reason that the CDS seller (protection buyer) makes regular payment to CDS buyer (protection seller) until a credit event happens. The TROR is more of a swap as payments are made by both the parties simultaneously and also it covers economic risk (including fluctuation in market interest rates).

Regards,
Sunil

 

[David Harper CFA FRM]

Hi Sunil,

On the apparent contradiction, Jorion refers to the difference (if the example is, say, a reference basket of 100 credits) between a 1st-to-default and a 99th- or 100th-to-default. On this issue (default correlation in the basket), we could refer to either a basket CDS or a CDO. You may find this post from last year helpful. So here we can equate:

high nth-to-default basket CDS ~ senior CDO tranches
medium nth-to-default ~ mezzanine CDO tranches
low nth-to-default (e.g., 1st-to-default) ~ junior/equity tranches

http://learn.bionicturtle.com/images/forum/cds_correlations.png

And now the "classic argument" is:
high correlation makes senior tranches (i.e., high n to default for basket CDS) more expensive (all other things equal) and junior tranches (e.g., 1st to default) less expensive;
low correlation makes senior tranches less expensive and junior tranches more expensive. You can see in my post that the binomial distribution can be used to illustrate this.

In a nutshell, if you have 100 credits with each 5% PD, consider a 100th-to-default (analogous to senior CDO tranche): if uncorrelated, the probability of triggering this basket CDS is virtually zero; = 5%^100 = ~ zero. Now increase correlation to 1.0 (perfect) and PD goes all the way up to 5%! Ergo, for the senior tranche, increase correlation increases the spread.

Now consider a 1st to default (junior tranche), what is the probability of triggering 1/100? Fully 99+% = 1-95%^100. Now increase correlation to perfect (1.0) and the probability DECREASES to only 5%! Ergo, for the junior tranche, increase correlation decreases the spread.

(The above is the classic line and the exam will not go further than this. If you are interested, smart folks at Kamakura have pushed this issue further).

"CDS is more of an option as compared to it being a swap."
Yes, agreed, it is sometimes called an option rather than a swap. But on the other hand, notice Hull's valuation consists of equating two swaps: the certain premium payments with the uncertain, contingent payoff. Aside from Culp, in my opinion, this point you make is why most authors use different terms to describe the counterparties. The TROR is truly a swap so you see payer/receiver, but the CDS is (arguably) a true credit derivative so you see protection buyer/seller.

"TROR is more of a swap as payments are made by both the parties simultaneously and also it covers economic risk (including fluctuation in market interest rates)."
Yes, true, so from a risk perspective, this is why Meissner shows that the TROR is a swap that covers more risk types (default, credit deterioration, and market risk). He would categorize a drop in interest rates as a MARKET RISK: The TROR hedges such a risk, the CDS does not. Further, the TROR hedges credit deterioration (downgrade) and a CDS may or may not (yes, if market to market, no if otherwise)

David

 

[frm_daniel]

Hi David,

Credit default swaps written on multiple names, the first-of-basket to default swap give the protection buyer to deliver one and only one defaulted security out of a baset of selected securites, ie the trigger event.What is the pay off to the protection buyer ? Does it cover the first default asset only ie.par minus the recovery value)?. If it is 9th to default swap, the cover amount will be on the 9th protected asset only (those defaults before 9th default assets will not be cover? Thus, spreads for 2rd to default swaps will be less than 1st to default swaps?


Regards,
Daniel

 

[David Harper CFA FRM]

Hi Daniel,

Yes, the nth-to-default is exactly as you say; e.g., in a 3rd-to-default, nothing happens upon the first two defaults in the basket (regardless of which credits default), then upon the 3rd default there is a credit event trigger and the buyer payoff is just like a single-name CDS: if physical, the protection buyer can deliver the defaulted credit and receive par/face, or if cash, the buyer receives LGD or "net loss" not gross loss (par/face of defaulted bond only minus recovery on defaulted bond only, not the basket). Either way, the protection buyer is receiving LGD (net loss) on the defaulted credit only, not the cumulative (in the vanilla design, anyway), just like a single name CDS.

So, ceteris paribus, the 3rd-to-default must earn the seller a lower premium than the 2nd-to-default which in turn must earn a lower premium than 1st-to-default (FTD).

The pricing of nth-to-default is very interesting as the correlation above enters strongly. For example, if the basket has 5 credits and each single name CDS has a premium of 20 bps, then if the default correlation is perfect (1.0), the FTD basket premium would also be 20 bps (default on 1 = default of all!); but if default correlation is zero, then FTD basket premium = ~ 100 bps (20 * 5) ... as above, lower correlation implies higer spread on the junior tranche (FTD CDS ~ equity tranche in CDO).

Now the 2nd-to-default, for the SAME GIVEN CORRELATION, must offer a lower premium. However, default/asset correlation is a very strong determinant; the 2nd-to-default premium could be higher than a FTD premium, if the basket is sufficiently large and the correlation is lower for the 2nd-to-D (or if it's a small basket, and the 2nd-to-default is more mezzanine, correlation can act the other way!)...so in regard to any mezzanine tranche (e.g., 2nd-to-default, 3rd-default) we generally say the response to correlation is "complicated" and depends on the particulars

David

 

[frm_daniel]

Hi David,

If I invested in the senior tranches asset, I am protected due to the subordination of credit enhancement for the senior claim. I will receive less coupon income compared with equity trench. If the assets have higher default correlation, it means senior tranches become more risky. Therefore, I have received less coupon income but to incur higher risk (with high assets default correlation) for the senior trench of asset I hold. However, I should be compensated with high risk I take. I see I have problem in the logic. Could you help?

Regards,
Daniel

 

[David Harper CFA FRM]

Hi Daniel,

I snapped a picture (with my new droid) from o'kanes
http://www.amazon.com/Modelling-Single-name-Multi-name-Derivatives-Finance/dp/0470519282/

What you say is exactly true of both dynamics (seniority and default correlation). They co-exist as inputs, so when talking about default correlation as a first pass, we typically really mean "impact of correlation for a given tranche (ceteris paribus)" and when talking about credit spread it's "credit spread up/down for a given correlation"

David

 

[[email protected]]

David,

So far we only learn about how the spread for Junior and senior tranches affected due to correlation of Zero and perfect correlation.

But can you please explain how is the spread changes if the default correlation is NEGATIVE?
and another scenario is the NUMBER of asset in the basket increase of decrease?

Thank you very much.

 

[David Harper CFA FRM]

Hi cheeseng82,

Negative is just a continuation into lower correlation.

Consider the junior tranche: From 1.0 to zero correlation, becomes more risky (expensive). Down to -1.0, and something almost certainly must default! Extreme risk

For the senior tranche, at -1.0 correlation is extremely safe because initial defaults are negatively correlated to imply no defaults on the rest. Extreme safety for the seniors.

In regard to numbers, I think this depends on how the question is phrased, i think answer can vary; i don't perceive a hard rule since numbers inform tranche widths.

David

 

[srinu2singaraju]

Hi David,

In a CDS basket there are 50 names and i entered in to 10th to Default swap. Up to 9 defaults i will not get receive anything from the protection seller.
Up on 10th default will i get paid on whole 50 names or it is from 1 to 10 names or it only for the 10th name.

Please clarify.

Thanks
srinivas

 

[David Harper CFA FRM]

Hi srinivas,

Let's say all the credits have a $1 million face value. In the 10th-to-default basket, no trigger for first nine defaults; upon 10th default, recovery is just like a single name CDS: protection seller pays $1 MM * (1 - recovery) ONLY on the 10th credit, not the prior nine.

On the other hand, a subordinated basket (as opposed to an nth-to-default basket) can be designed to pay cumulatively; e.g., for up to 10 defaults; but this will typically have caps (per default and cumulatively)...otherwise is would be similar to ten single name CDS

David

 

[srinu2singaraju]

Hi David,
Thanks for the quick response.
One more doubt- My understanding on Basket CDS is i am buying protection for the whole basket and in that will get paid if the 10th to default occurs.

 

[[email protected]]

Hi Daniel,

Yes, the nth-to-default is exactly as you say; e.g., in a 3rd-to-default, nothing happens upon the first two defaults in the basket (regardless of which credits default), then upon the 3rd default there is a credit event trigger and the buyer payoff is just like a single-name CDS: if physical, the protection buyer can deliver the defaulted credit and receive par/face, or if cash, the buyer receives LGD or "net loss" not gross loss (par/face of defaulted bond only minus recovery on defaulted bond only, not the basket). Either way, the protection buyer is receiving LGD (net loss) on the defaulted credit only, not the cumulative (in the vanilla design, anyway), just like a single name CDS.

So, ceteris paribus, the 3rd-to-default must earn the seller a lower premium than the 2nd-to-default which in turn must earn a lower premium than 1st-to-default (FTD).

The pricing of nth-to-default is very interesting as the correlation above enters strongly. For example, if the basket has 5 credits and each single name CDS has a premium of 20 bps, then if the default correlation is perfect (1.0), the FTD basket premium would also be 20 bps (default on 1 = default of all!); but if default correlation is zero, then FTD basket premium = ~ 100 bps (20 * 5) ... as above, lower correlation implies higer spread on the junior tranche (FTD CDS ~ equity tranche in CDO).

Now the 2nd-to-default, for the SAME GIVEN CORRELATION, must offer a lower premium. However, default/asset correlation is a very strong determinant; the 2nd-to-default premium could be higher than a FTD premium, if the basket is sufficiently large and the correlation is lower for the 2nd-to-D (or if it's a small basket, and the 2nd-to-default is more mezzanine, correlation can act the other way!)...so in regard to any mezzanine tranche (e.g., 2nd-to-default, 3rd-default) we generally say the response to correlation is "complicated" and depends on the particulars

David

Hi David,

I have been a member since the past 4 months and have found this forum very informative. I was searching the internet regarding correlation in nth to default CDS and found this thread. Just wanted to extend the logic for pricing nth to default and ask a question on it. Suppose I have a 3rd to default CDS and even the basket has 3 reference obligations(credits). Also suppose the 3 reference obligations have a premium of 10 bps, 20 bps and 30 bps. In this particular case what would be the 3rd to default basket premium for a default correlation of zero and also for a default correlation of 1.0(perfect). Thank you. Regards.