Hi David,
Trying to get the whole idea of book 5, I found something that sounds weird: (previously have looked through the existing threads and there is no discussion about this)
On reading "When selling becomes viral" (current issues) the author gives 2 ideas :
1st: during the Covid crisis, Investment grade (IG) bonds and High Yield (HY) bonds experienced similar increases (declines) in their spreads (prices), higher than 500bps.
2nd: during the GFC, HY bonds experienced a much higher decline in prices (increase in spreads) that IG bonds.
With this, I understand there could be 2 different scenarios/reactions to a crisis.
The confusion comes when mixing it with the reading of “factors”. Here, it is demonstrated that IG bonds experienced a high increase in returns in recessions (which matches with what happened during GCF and COVID crisis), but…HY bonds does not experience an increase in returns, but a decline, which does not match with the Idea I got from what happened neither in the GFC nor during COVID crisis.
How can this be understood? Maybe I am mixing the spread concept with the return/yield concept? Both are negatively correlated with prices, right? Could you help me to grab the right concept?
Thanks a lot in advance!
Trying to get the whole idea of book 5, I found something that sounds weird: (previously have looked through the existing threads and there is no discussion about this)
On reading "When selling becomes viral" (current issues) the author gives 2 ideas :
1st: during the Covid crisis, Investment grade (IG) bonds and High Yield (HY) bonds experienced similar increases (declines) in their spreads (prices), higher than 500bps.
2nd: during the GFC, HY bonds experienced a much higher decline in prices (increase in spreads) that IG bonds.
With this, I understand there could be 2 different scenarios/reactions to a crisis.
The confusion comes when mixing it with the reading of “factors”. Here, it is demonstrated that IG bonds experienced a high increase in returns in recessions (which matches with what happened during GCF and COVID crisis), but…HY bonds does not experience an increase in returns, but a decline, which does not match with the Idea I got from what happened neither in the GFC nor during COVID crisis.
How can this be understood? Maybe I am mixing the spread concept with the return/yield concept? Both are negatively correlated with prices, right? Could you help me to grab the right concept?
Thanks a lot in advance!

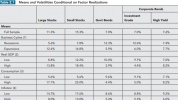
 That is a potentially complicated comparison, but I would start with: one of the key observations in Haddad's paper is that the the investment grade (IG) bonds were dysfunctional; e.g., "These observations suggest that the investment-grade market in particular, which is the core funding market for US companies and totals over $7 trillion, was dysfunctional; we more sharply characterize this dysfunction in Section 3." You could argue Haddad and Ang are in the same direction w.r.t. IG bonds during recession: Ang shows they have a positive reaction (12.6%) while Haddad says the sudden spread widening (aka, negative CDS basis: the CDS spreads didn't spike) was dysfunctional and not expected. Secondly, it's really important to keep in mind that each of them are making inferences from a certain sample (aka, historical period). Haddad is clearly not generalizing into Factor theory. Ang copied below just for my own reference (emphasis mine)
That is a potentially complicated comparison, but I would start with: one of the key observations in Haddad's paper is that the the investment grade (IG) bonds were dysfunctional; e.g., "These observations suggest that the investment-grade market in particular, which is the core funding market for US companies and totals over $7 trillion, was dysfunctional; we more sharply characterize this dysfunction in Section 3." You could argue Haddad and Ang are in the same direction w.r.t. IG bonds during recession: Ang shows they have a positive reaction (12.6%) while Haddad says the sudden spread widening (aka, negative CDS basis: the CDS spreads didn't spike) was dysfunctional and not expected. Secondly, it's really important to keep in mind that each of them are making inferences from a certain sample (aka, historical period). Haddad is clearly not generalizing into Factor theory. Ang copied below just for my own reference (emphasis mine)