Confidence Interval for VaR

[MSharky]

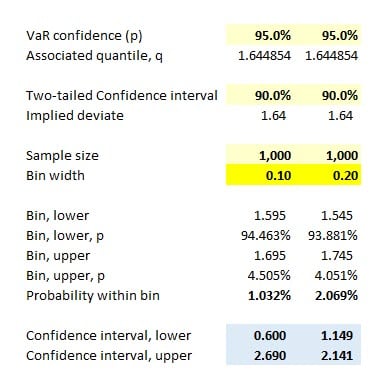
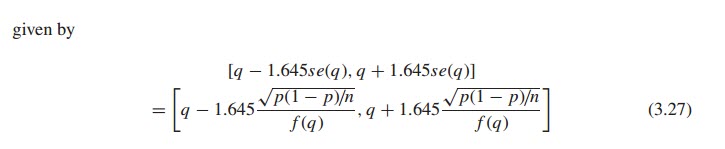When calculating a confidence interval for VaR, we need to take into account the bin size (i.e. the width of the rectangles in the histogram bars). Why is it when we increase the bin size, this reduces the length of the confidence interval? I am trying to think about it from an intuitive perspective. If the bins are wider, wouldn't that mean that VaR is more uncertain now, since they can take on a wider range of values.


Thanks,

M.S.

 

[[email protected]]

Hi David...one query I had while going thru this topic is increasing the bin size shall reduce std error but how can the confidence interval narrow....shouldn't it broaden???

 

[David Harper CFA FRM]

Hi @meenalbaheti In Dowd's approach (derived on page 70-71 of his book, the assignment, at https://forum.bionicturtle.com/resources/kevin-dowd-measuring-market-risk.87/) the bin width is an "arbitrary" parameter (it is the weak spot here!) which informs the denominator, in 3.27 (below), of the fraction which is the standard error. f(q) is the probability mass within the bin range. In this way, increasing the bin, increases the probability mass, which decreases the standard error and hence the confidence interval.

Here is Dowd's example, importantly which is using the known normal merely to illustrate (!), where he increase the bin from h = 0.10 to h = 0.20. I hope that's helpful. Here is my XLS https://www.dropbox.com/s/k8qrc1dfoii99zb/0924-bin-width.xlsx?dl=0

@Nicole Seaman I do think this Study Note (i.e., Dowd's Chapter 3 and 4; the first reading in P2.T5 Market Risk) would really benefit from an update by Deepa (a few of these LOs are too short), perhaps we can put this in her queue? Thanks!

 

[[email protected]]

Thanks David...the illustration was helpful..