Hi @David Harper CFA FRM ,
Firstly thanks a lot for replying to all of my previous questions. I have one more for you.
While going through the calculation for Credit Support Amount, I have the following Query.
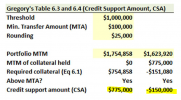
In the Notes, the formula for Hypothetical Collateral Amount is stated as MAX(MTM- T, 0)- MAX(-MTM-T , 0) -C
However wouldn't the term MAX(-MTM-T, 0) always amount to 0, since threshold will always be positive ?
Is my interpretation correct ?
Also I have attached an Excel sheet detailing the above calculation. Would really appreciate if you could confirm the calculation and the formulas.
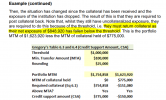
If it is correct, then the value of Portfolio on DAY 3 has fallen down to 800000. However the formula states the credit support amount to be 0.
Since our portfolio has already fallen below 1000000, wouldn't we re be required to deposit the collateral in this case ?
Thanks.
Firstly thanks a lot for replying to all of my previous questions. I have one more for you.

While going through the calculation for Credit Support Amount, I have the following Query.
In the Notes, the formula for Hypothetical Collateral Amount is stated as MAX(MTM- T, 0)- MAX(-MTM-T , 0) -C
However wouldn't the term MAX(-MTM-T, 0) always amount to 0, since threshold will always be positive ?
Is my interpretation correct ?
Also I have attached an Excel sheet detailing the above calculation. Would really appreciate if you could confirm the calculation and the formulas.
If it is correct, then the value of Portfolio on DAY 3 has fallen down to 800000. However the formula states the credit support amount to be 0.
Since our portfolio has already fallen below 1000000, wouldn't we re be required to deposit the collateral in this case ?
Thanks.
Attachments
Last edited: