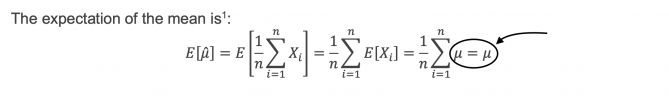You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Chapter 5 Sample moments
- Thread starter DenisAmbrosov
- Start date
-
- Tags
- sample-moments
Lu Shu Kai FRM
Well-Known Member
Hi @DenisAmbrosov ,
From left to right, the sum of the population mean over n iterations divided by n equals the population mean.
Not too sure what your question is, perhaps you can be more specific?
From left to right, the sum of the population mean over n iterations divided by n equals the population mean.
Not too sure what your question is, perhaps you can be more specific?
DenisAmbrosov
New Member
I just can't understand. E[mu-hat]. Why mu-hat? As I understand mu-hat is for sample mean.But here I have E[mu-hat(sample mean)] = population meanHi @DenisAmbrosov ,
From left to right, the sum of the population mean over n iterations divided by n equals the population mean.
Not too sure what your question is, perhaps you can be more specific?
Lu Shu Kai FRM
Well-Known Member
Dear @DenisAmbrosov ,
I think the math is trying to say - the expectation of the sample mean or the average of many sample means should give you the population mean, thanks.
I think the math is trying to say - the expectation of the sample mean or the average of many sample means should give you the population mean, thanks.
DenisAmbrosov
New Member
I got it. Thank you!Dear @DenisAmbrosov ,
I think the math is trying to say - the expectation of the sample mean or the average of many sample means should give you the population mean, thanks.
DenisAmbrosov
New Member
Lu Shu Kai FRM
Well-Known Member
Hi @DenisAmbrosov ,
The term asymptotically unbiased just explains the math in words. The word asymptotically comes from the word asymptote, which is a line that the curve seems to approach as it approaches infinity, but never really touches. The same with the estimator, as the sample size goes to infinity, the estimator becomes unbiased - never overestimating or underestimating the population statistic.
The term asymptotically unbiased just explains the math in words. The word asymptotically comes from the word asymptote, which is a line that the curve seems to approach as it approaches infinity, but never really touches. The same with the estimator, as the sample size goes to infinity, the estimator becomes unbiased - never overestimating or underestimating the population statistic.
Hello @David Harper CFA FRM , I think that there are an error in the example of third moment in chapter five, book 2. I understand that the skewness sample it has to be 0.198, isn’t? See picture attached below.
Regards.
Regards.
Attachments
Hello again @David Harper CFA FRM , also I couldn’t get to the results of the example for the fourth moment in chapter 5, book 2. See picture below.
Attachments
HI @JGURR5668 Not errors. For skew, notice I matched to Excel's skew per the "Excel F()" below; the sample skew shouldn't be smaller than the population skew (0.198 <? 0.201). So the adjustment used is 19.8*100/[(100 - 1)*(100-2)]/1.0^3 = 0.2040x and this sample skew is greater than the population skew. In the case of kurtosis, similar logic but I just used Excel's KURT function, see adjustment here https://support.microsoft.com/en-us/office/kurt-function-bc3a265c-5da4-4dcb-b7fd-c237789095ab Thanks,
Hello David, thanks for your answer but I can’t get to the same results that you have in the notes, could you indicate me where can I find the excel with your estimation to see which is my mistake please? Or if you can tell me what it is the operation that I’m doing wrong in the excercise that I attached above? I’d appreciate.
Regards.
Regards.
HI @JGURR5668 Here are the two sheets (but keep in mind that the simulated panel has random numbers so generates a new set each time) https://www.dropbox.com/s/udmnbogicmejhzx/3rd_4th-moments.xlsx?dl=0
Similar threads
- Replies
- 5
- Views
- 2K
- Replies
- 0
- Views
- 478
- Replies
- 0
- Views
- 233
- Replies
- 9
- Views
- 2K
- Replies
- 0
- Views
- 115