DenisAmbrosov
New Member
What does 'If a normal distribution is time-varying, then its unconditional distribution will be heavy-tailed.' mean?
Chapter 1 Measure of financial risk
- Thread starter DenisAmbrosov
- Start date
DenisAmbrosov
New Member
Why the VaR (y axis) increases with the confidence level (x axis) for a standard normal distribution.?
Lu Shu Kai FRM
Well-Known Member
Hi @DenisAmbrosov ,
With regards to your first question:
An unconditional distribution is, as its name suggests, is the probability distribution of an event that takes place without taking into consideration other events that have taken/not taken place or conditions present.
The mean-variance framework (or modern portfolio theory) assumes that asset returns are normally distributed. However, the distribution of the asset returns changes over time (or is time-varying), which suggests that its unconditional distribution (without taking into consideration anything) will be heavy-tailed.
With regards to your first question:
An unconditional distribution is, as its name suggests, is the probability distribution of an event that takes place without taking into consideration other events that have taken/not taken place or conditions present.
The mean-variance framework (or modern portfolio theory) assumes that asset returns are normally distributed. However, the distribution of the asset returns changes over time (or is time-varying), which suggests that its unconditional distribution (without taking into consideration anything) will be heavy-tailed.
Lu Shu Kai FRM
Well-Known Member
Hi @DenisAmbrosov ,
With regards to your second question:
That's how VaR works. The VaR quantity is a percentile-based risk measure that takes the maximum loss based on a confidence level over a period of time. If you have a number set of losses, say:
{-100, -90, -80 ... 0}
Then your VaR of 90% confidence level would be -90 because that is the "90% worst scenario". In the case of your picture, the losses are treated as positive numbers for the sake of convention. The loss distributions in VaR tend to be represented as positive numbers for ease of interpretation, thanks.
Hope that clarifies.
EDIT:
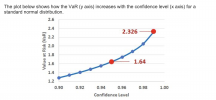
I think your picture is also quite special because in this case it is quoting the normal distribution deviate, which David places great emphasis on. For a 95% and 99% percentile, it references the normal deviation deviate z = 1.645 and 2.326, which are the two numbers on your picture.
With regards to your second question:
That's how VaR works. The VaR quantity is a percentile-based risk measure that takes the maximum loss based on a confidence level over a period of time. If you have a number set of losses, say:
{-100, -90, -80 ... 0}
Then your VaR of 90% confidence level would be -90 because that is the "90% worst scenario". In the case of your picture, the losses are treated as positive numbers for the sake of convention. The loss distributions in VaR tend to be represented as positive numbers for ease of interpretation, thanks.
Hope that clarifies.
EDIT:
I think your picture is also quite special because in this case it is quoting the normal distribution deviate, which David places great emphasis on. For a 95% and 99% percentile, it references the normal deviation deviate z = 1.645 and 2.326, which are the two numbers on your picture.
DenisAmbrosov
New Member
Thanks for the reply! To tell the truth, I am still not comfortable with it. If it is possible, may you explain it in detail, please
Also, some good notes about the picture I attached, if you somewhat extend your explanation on this point as well I will be happy.
Thanks
DenisAmbrosov
New Member
Why 'The more illiquid the market, the longer the relevant holding period' is so?[VaR]
DenisAmbrosov
New Member
Why is 'When μ = 0, the VaR rises with the square root of the holding period'?
Lu Shu Kai FRM
Well-Known Member
Hi @DenisAmbrosov ,
With regards to your questions, most of them can be answered by simply - 1. Searching the forum, 2. Searching Google or 3. Thinking deeper about your problems. You shouldn't ask every question the first time it pops up in your head, it won't help you that way.
With regards to your third and fourth question:
- If the market for an asset is illiquid, you won't be able to sell or buy it immediately and the period you hold it for is longer.
- If a portfolio has mu = 0.5 vs mu = 0, the loss distribution of that portfolio will be skewed left (in the case of a loss distribution where losses are represented positively) and the maximum losses would be lower for most percentiles (or in this case, per holding period).
With regards to your questions, most of them can be answered by simply - 1. Searching the forum, 2. Searching Google or 3. Thinking deeper about your problems. You shouldn't ask every question the first time it pops up in your head, it won't help you that way.
With regards to your third and fourth question:
- If the market for an asset is illiquid, you won't be able to sell or buy it immediately and the period you hold it for is longer.
- If a portfolio has mu = 0.5 vs mu = 0, the loss distribution of that portfolio will be skewed left (in the case of a loss distribution where losses are represented positively) and the maximum losses would be lower for most percentiles (or in this case, per holding period).
Hi @DenisAmbrosov (epic thank you @lushukai for your patience and your expertise ... and your wisdom too!). I do agree with Lu Shu's advice (darn, I can't find a way to disagree with you lately 
)...
Your first (1st) question is definitely the hardest (of your four), as it requires clarity on conditional versus unconditional distribution in the time series context. I like to think of a skier going down a flat bunny slope and carving out her dispersion (volatility). If her instantaneous volatility is normal and she skis in a straight line, you'd see a roughly normal carve out. But if she swerves left and right (time varying mean) and her dispersion also varies (time varying volatility, her volatility is volatile!), then when she's done, the carve out is going to have "fat edges." That's just a very loose metaphor for a harder mathematical idea.
Your second and fourth question should be easy once you master our essential absolute normal VaR formula:
Your third is an important concept in practice. I hold many large cap stocks, like Elastic (ESTC) is my largest holding. What should be my VaR horizon? It can be short because I can exit that position so fast that it's sort of amazing (I can get out it seconds). It can be short here because it's possible for me to realize my (worst expected) loss quickly. For traded equities, 10-day VaR (or 1-day is common). But what about an illiquid (eg, RE or PE) position? Can't use 1-day VaR because there's almost no such thing as a 1-day non-paper loss: it will take time to realize a loss (or a gain). VaR wants to know the worst expected loss with some confidence: an illiquid position, by definition, implies we will take longer to exit and realize any loss. A 1-day paper loss doesn't matter if it takes 10 days (or longer) to exit the position. Spoiler alert: in P2, we review a liquidity-adjusted VaR that adjusts based on the time required to liquidate. In fact, we will distinguish a different type of liquidity factor/risk (i.e., endogenous liquidity-adjusted VaR) that increases the VaR precisely because an exit of the position will take more time and/or probably put downward pressure on the price in the meantime. The horizon and impact of exiting illiquid positions mattes. So this concept has a quantitative implement. Hope that's helpful,
)...... especially here in the forum, each of your questions has been asked/answered, in some cases many times.
Your first (1st) question is definitely the hardest (of your four), as it requires clarity on conditional versus unconditional distribution in the time series context. I like to think of a skier going down a flat bunny slope and carving out her dispersion (volatility). If her instantaneous volatility is normal and she skis in a straight line, you'd see a roughly normal carve out. But if she swerves left and right (time varying mean) and her dispersion also varies (time varying volatility, her volatility is volatile!), then when she's done, the carve out is going to have "fat edges." That's just a very loose metaphor for a harder mathematical idea.
Your second and fourth question should be easy once you master our essential absolute normal VaR formula:
- single period: aVaR = µ + σ*Z
- multi period: aVaR = µ*Δt + σ*Z*sqrt(Δt); and relative VaR drops the drift:
- multi period rVaR = σ*Z*sqrt(Δt)
Your third is an important concept in practice. I hold many large cap stocks, like Elastic (ESTC) is my largest holding. What should be my VaR horizon? It can be short because I can exit that position so fast that it's sort of amazing (I can get out it seconds). It can be short here because it's possible for me to realize my (worst expected) loss quickly. For traded equities, 10-day VaR (or 1-day is common). But what about an illiquid (eg, RE or PE) position? Can't use 1-day VaR because there's almost no such thing as a 1-day non-paper loss: it will take time to realize a loss (or a gain). VaR wants to know the worst expected loss with some confidence: an illiquid position, by definition, implies we will take longer to exit and realize any loss. A 1-day paper loss doesn't matter if it takes 10 days (or longer) to exit the position. Spoiler alert: in P2, we review a liquidity-adjusted VaR that adjusts based on the time required to liquidate. In fact, we will distinguish a different type of liquidity factor/risk (i.e., endogenous liquidity-adjusted VaR) that increases the VaR precisely because an exit of the position will take more time and/or probably put downward pressure on the price in the meantime. The horizon and impact of exiting illiquid positions mattes. So this concept has a quantitative implement. Hope that's helpful,
Last edited:
DenisAmbrosov
New Member
I got it! Sorry for this. I will ask only those questions which I will not figure out by myself! I am still a student, so I love asking too many questions but I see your point.Hi @DenisAmbrosov (epic thank you @lushukai for your patience and your expertise ... and your wisdom too!). I do agree with Lu Shu's advice (darn, I can't find a way to disagree with you lately
... especially here in the forum, each of your questions has been asked/answered, in some cases many times.
Your first (1st) question is definitely the hardest (of your four), as it requires clarity on conditional versus unconditional distribution in the time series context. I like to think of a skier going down a flat bunny slope and carving out her dispersion (volatility). If her instantaneous volatility is normal and she skis in a straight line, you'd see a roughly normal carve out. But if she swerves left and right (time varying mean) and her dispersion also varies (time varying volatility, her volatility is volatile!), then when she's done, the carve out is going to have "fat edges." That's just a very loose metaphor for a harder mathematical idea.
Your second and fourth question should be easy once you master our essential absolute normal VaR formula:
We have hundreds (thousands?) of threads on VaR, so please don't immediately follow up with me. I'm just saying that you goal is mastery over this essential formula, were Z = 1.645 if the distribution is normal and our sought confidence is 95.0%. Higher confidence is reflected in a higher multiple, Z, of the standard deviation. You want (and need) fluency in that.
- single period: aVaR = µ + σ*Z
- multi period: aVaR = µ*Δt + σ*Z*sqrt(Δt); and relative VaR drops the drift:
- multi period rVaR = σ*Z*sqrt(Δt)
Your third is an important concept in practice. I hold many large cap stocks, like Elastic (ESTC) is my largest holding. What should be my VaR horizon? It can be short because I can exit that position so fast that it's sort of amazing (I can get out it seconds). It can be short here because it's possible for me to realize my (worst expected) loss quickly. For traded equities, 10-day VaR (or 1-day is common). But what about an illiquid (eg, RE or PE) position? Can't use 1-day VaR because there's almost no such thing as a 1-day non-paper loss: it will take time to realize a loss (or a gain). VaR wants to know the worst expected loss with some confidence: an illiquid position, by definition, implies we will take longer to exit and realize any loss. A 1-day paper loss doesn't matter if it takes 10 days (or longer) to exit the position. Spoiler alert: in P2, we review a liquidity-adjusted VaR that adjusts based on the time required to liquidate. In fact, we will distinguish a different type of liquidity factor/risk (i.e., endogenous liquidity-adjusted VaR) that increases the VaR precisely because an exit of the position will take more time and/or probably put downward pressure on the price in the meantime. The horizon and impact of exiting illiquid positions mattes. So this concept has a quantitative implement. Hope that's helpful,
Thank you!
Thank you @DenisAmbrosov for accepting feedback graciously. I'm still a (lifelong) student, too I love questions, questions in the forum is how I became "expert", so don't want to discourage what is a maybe the finest art in learning! Thanks,
I love questions, questions in the forum is how I became "expert", so don't want to discourage what is a maybe the finest art in learning! Thanks,Similar threads
