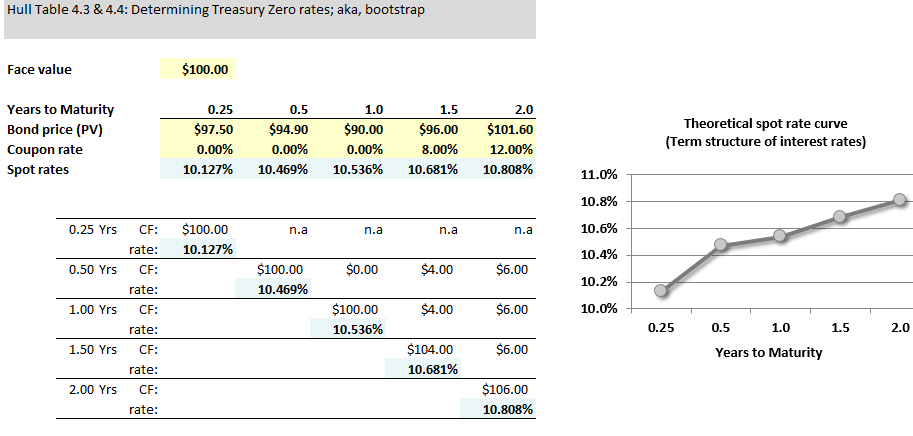
Hello. It looks like we compute discount factors using bond prices and the maturing par value and we compute bond prices by discounting the cash flows using discount factors (or spot which are derived from discount factors). Isn't this going in a loop?
Sounds stupid, but in real life, what information gets provided first? Discount factors or bond prices?
Thx,
Glen
Sounds stupid, but in real life, what information gets provided first? Discount factors or bond prices?
Thx,
Glen


 ... so bootstrap is a verb referring to a method that assists in retrieving a spot rate (or discount factor, as they are virtually synonymous). I hope that helps!
... so bootstrap is a verb referring to a method that assists in retrieving a spot rate (or discount factor, as they are virtually synonymous). I hope that helps!