Hi david
In calculating the size of up move factor U wat does square root of t mean is it time to maturity or the length of the step in the binomial model.
for example to calculate the value of a 6 month american call option using a 2 step binomial model wat will be the t value taken here to calculate U.
THANKS.
In calculating the size of up move factor U wat does square root of t mean is it time to maturity or the length of the step in the binomial model.
for example to calculate the value of a 6 month american call option using a 2 step binomial model wat will be the t value taken here to calculate U.
THANKS.


 In case you want to see it "in action," I pulled out the above example (from the learning XLS) to a single sheet here at
In case you want to see it "in action," I pulled out the above example (from the learning XLS) to a single sheet here at 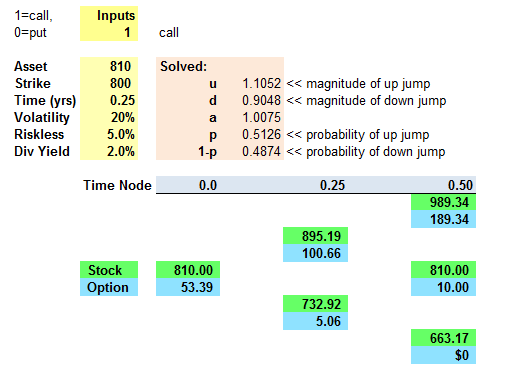
 I just happen to be currently revising these binomial exhibits, I think they look better (eg, including some formulas in the exhibit):
I just happen to be currently revising these binomial exhibits, I think they look better (eg, including some formulas in the exhibit):