Binomial Options Valuation Question
- Thread starter bhar
- Start date
bhar You have considered only one case of UU, however several combinations are possible via UD, DU, DD, UU
UD: 40*1.2*(1/1.2)=40, value=40-37=3 net value after probability=3*Pu*Pd=3*.67*.33=.67
DU: 40*1.2*(1/1.2)=40, value=40-37=3 net value after probability=3*Pu*Pd=.67
DD: 40*(1/1.2)*(1/1.2)=27.77, value=27.7-37=0 net value after probability=0*Pd*Pd=0*.33*.33=0
UU: 40*1.2*(1.2)=57.76, value=57.76-37=20.76 net value after probability=20.76*Pu*Pu=3*.67*.67=9.319
net value in PV terms
=(.67+.67+0+9.319)*e^(-0.08*.25)
=(10.659)*e^(-0.08*.25)
=10.659*.98
=10.445 approx.
thanks
UD: 40*1.2*(1/1.2)=40, value=40-37=3 net value after probability=3*Pu*Pd=3*.67*.33=.67
DU: 40*1.2*(1/1.2)=40, value=40-37=3 net value after probability=3*Pu*Pd=.67
DD: 40*(1/1.2)*(1/1.2)=27.77, value=27.7-37=0 net value after probability=0*Pd*Pd=0*.33*.33=0
UU: 40*1.2*(1.2)=57.76, value=57.76-37=20.76 net value after probability=20.76*Pu*Pu=3*.67*.67=9.319
net value in PV terms
=(.67+.67+0+9.319)*e^(-0.08*.25)
=(10.659)*e^(-0.08*.25)
=10.659*.98
=10.445 approx.
thanks
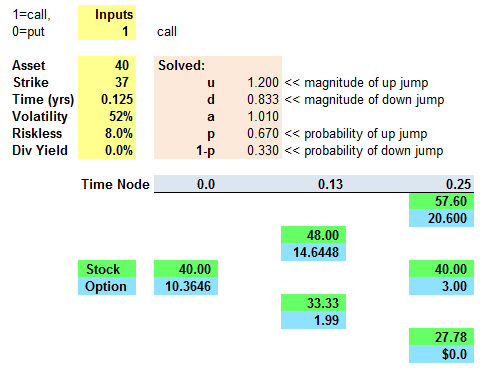
@Shakti, I come pretty close to that, I think you meant 57.60 forUU:
David Harper, CFA, FRM, CIPM
Yeah I agree david
40*1.2*(1.2)=57.6 not 57.76 so yeah a bit of error in my calculation.
20.6*Pu*Pu=20.6*.67*.67=9.247
=(.67+.67+0+9.247)*e^(-0.08*.25)
=(10.58734)*e^(-0.08*.25)
=10.58734*.98
=10.376 approx.
thanks
Yeah I agree david
40*1.2*(1.2)=57.6 not 57.76 so yeah a bit of error in my calculation.
20.6*Pu*Pu=20.6*.67*.67=9.247
=(.67+.67+0+9.247)*e^(-0.08*.25)
=(10.58734)*e^(-0.08*.25)
=10.58734*.98
=10.376 approx.
thanks
Should the time be .25 instead of .125 as you have taken. Please ignore. Shot it out too fast. It was solved as 45/360 or .25/2@Shakti, I come pretty close to that, I think you meant 57.60 forUU:
Thanks
bhar, i followed Shakti and assumed the option has a 3 month maturity, but I was not sure. The question is unclear because the (t) can either refer to
- t = time step
- t = time to expiration
bhar furthermore as it is an European call option we can exercise the option at maturity only so that we need to consider the different values that option can take at maturity only. So that we discount the final values for time to maturity that is 3 months or t=.25 yrs. I hope you understood.
thanks
thanks
ABFRM
Member
@ David i think we have to use d=0.8 rather than 0.833 because in HULL if volatility is given then we can calculate the d=1/u. yeah it doesnt make significant difference but i think for larger values it will.
ABFRM
Member
i think when t is given we should take it as a time step becuase every book follows if they want to talk about maturity they will talk about T. i dont know but i think u have to check the question again from which source Bhar has taken the question.
so like Hull follows
so like Hull follows
- t = time step
- T = time to expiration or time to maturity.
Hi Abhishek,
- Given the lack of assumptions, I think you could assume either d = 0.8 or d = 1/1.2, as both Shakti and I did. I don't think the key is whether volatility is provided. It's a choice between an assumption, which is not stated, as to whether prices are normal (arithmetic, if you will) or lognormal (geometric). To assume d = 1/1.2 is to assume a binomial that converges on BSM and its lognormal price assumption
- In regard to (t) versus (T), excellent observation, I frankly did not think of that! Sweet attention to detail.
Hi David
In the practise questions for Binomial Trees- this is the awsner below as per ur pdf, Can you kindly explain how you got $ 3.5 pls ? Im totally stumped on that step and have been scribbling for last few hrs without understanding the formula behind that. Im assuming the 1% is derived by r.f * time ie 0.04 * 0.25 = 1% .thanks
19.12.1 C. $1.53
Following Hull, a riskless portfolio consists of long delta (d) shares + short one option.
If the stock moves up, value of the riskless portfolio = $13*delta - $3 loss on the written call option; and if the stock moves down, value of the riskless portfolio = $7*delta. Setting them equal (i.e., riskless payoff): $13*d - $3 = $7*d, and 6d =3, so d = 0.5.
If delta (d) = 0.5, then value of portfolio today is: $10*0.5 - f = 5 -f = $3.5*exp(-1%), such that
f = 5 - 3.5*exp(-1%) = $1.53483
Amit
In the practise questions for Binomial Trees- this is the awsner below as per ur pdf, Can you kindly explain how you got $ 3.5 pls ? Im totally stumped on that step and have been scribbling for last few hrs without understanding the formula behind that. Im assuming the 1% is derived by r.f * time ie 0.04 * 0.25 = 1% .thanks
19.12.1 C. $1.53
Following Hull, a riskless portfolio consists of long delta (d) shares + short one option.
If the stock moves up, value of the riskless portfolio = $13*delta - $3 loss on the written call option; and if the stock moves down, value of the riskless portfolio = $7*delta. Setting them equal (i.e., riskless payoff): $13*d - $3 = $7*d, and 6d =3, so d = 0.5.
If delta (d) = 0.5, then value of portfolio today is: $10*0.5 - f = 5 -f = $3.5*exp(-1%), such that
f = 5 - 3.5*exp(-1%) = $1.53483
Amit
Hi David
I actually finally got the awnser to the above question, so no worries with the formulas but has lead me to another general question based on the solution pls.
Notationally,
u = 13/10 = 1.3; d = 7/10 = 0.7
p = [exp(rt) - d]/[u-d] = [exp(1%) - 0.7]/(1.3 - 0.9) = 0.51675
f = exp(-rT)*[0.51675*$3 + 0) = $1.53483
Ie this statement of Following Hull, a riskless portfolio consists of long delta (d) shares + short one option.
So here in such a similar question do we always assume the portfolio is a riskless one and that it has been hedged correctly and shouldnt the d = 0.7 in the formula above ? ( i guess its a typo )?
thanks
Amit
I actually finally got the awnser to the above question, so no worries with the formulas but has lead me to another general question based on the solution pls.
Notationally,
u = 13/10 = 1.3; d = 7/10 = 0.7
p = [exp(rt) - d]/[u-d] = [exp(1%) - 0.7]/(1.3 - 0.9) = 0.51675
f = exp(-rT)*[0.51675*$3 + 0) = $1.53483
Ie this statement of Following Hull, a riskless portfolio consists of long delta (d) shares + short one option.
So here in such a similar question do we always assume the portfolio is a riskless one and that it has been hedged correctly and shouldnt the d = 0.7 in the formula above ? ( i guess its a typo )?
thanks
Amit
hi
value of portfolio=V=long delta (d) shares + short one option
delta=C2-C1/S2-S1
let S goes from S to following in next step,
S->S+(up) or S->S-(down)
delta*(S+) - C+=delta*(S-) -C (same pay in either state for risk-less portfolio)
=>delta*(S+)-delta*(S-)=C+ - C-
delta=(C+ - C-)/(S+ - S-)
so payoff for up state= delta*(S+) - C+=[(C+ - C-)/(S+ - S-)*(S+)] - C+=[(C+ - C-)*(S+) - C+(S+ - S-)]/(S+ - S-)=[(C+*S-) - (C-*(S+))]/(S+ - S-)
so payoff for down state= delta*(S-) - C-=[(C+ - C-)/(S+ - S-)*(S-)] - C-=[(C+ - C-)*(S-)- C-*(S+ - S-)]/(S+ - S-)=C+*(S-)-( C-*(S+ )/(S+ - S-) which is same as above.
so assuming this delta for every step of the binomial tree will result in the risk-less return that is same return in either of the two branches of the tree. we have verifies that the portfolio is hedge correctly for the above value of delta.
thanks
value of portfolio=V=long delta (d) shares + short one option
delta=C2-C1/S2-S1
let S goes from S to following in next step,
S->S+(up) or S->S-(down)
delta*(S+) - C+=delta*(S-) -C (same pay in either state for risk-less portfolio)
=>delta*(S+)-delta*(S-)=C+ - C-
delta=(C+ - C-)/(S+ - S-)
so payoff for up state= delta*(S+) - C+=[(C+ - C-)/(S+ - S-)*(S+)] - C+=[(C+ - C-)*(S+) - C+(S+ - S-)]/(S+ - S-)=[(C+*S-) - (C-*(S+))]/(S+ - S-)
so payoff for down state= delta*(S-) - C-=[(C+ - C-)/(S+ - S-)*(S-)] - C-=[(C+ - C-)*(S-)- C-*(S+ - S-)]/(S+ - S-)=C+*(S-)-( C-*(S+ )/(S+ - S-) which is same as above.
so assuming this delta for every step of the binomial tree will result in the risk-less return that is same return in either of the two branches of the tree. we have verifies that the portfolio is hedge correctly for the above value of delta.
thanks
Hi Amit,
You are correct about the typo, it should be: p = [exp(rt) - d]/[u-d] = [exp(1%) - 0.7]/(1.3 - 0.7) = 0.51675
(I updated the source, tagged for revision to PDF: http://forum.bionicturtle.com/threads/p1-t4-1-one-and-two-step-binomial-valuation-models.4744/)
With respect to "do we always assume the portfolio is a riskless one?" ... in this procedure (also as reflected in Shakti's calculations), by design, we are constructing a portfolio which has the same payoff in either of the only two outcomes (also, a simplifying design decision!). In this question, delta = 0.5, gives us a portfolio (long 0.5 share plus short one call option) that has a future payoff of the same $3.5 in either future outcome. That is by design, so that we can then discount by the risk-free rate: we are allowed to discount by the risk-free rate precisely because we are certain about the future payoff (i.e., it has no variability, it has expected value of 3.5 with variance of zero). Thanks,
You are correct about the typo, it should be: p = [exp(rt) - d]/[u-d] = [exp(1%) - 0.7]/(1.3 - 0.7) = 0.51675
(I updated the source, tagged for revision to PDF: http://forum.bionicturtle.com/threads/p1-t4-1-one-and-two-step-binomial-valuation-models.4744/)
With respect to "do we always assume the portfolio is a riskless one?" ... in this procedure (also as reflected in Shakti's calculations), by design, we are constructing a portfolio which has the same payoff in either of the only two outcomes (also, a simplifying design decision!). In this question, delta = 0.5, gives us a portfolio (long 0.5 share plus short one call option) that has a future payoff of the same $3.5 in either future outcome. That is by design, so that we can then discount by the risk-free rate: we are allowed to discount by the risk-free rate precisely because we are certain about the future payoff (i.e., it has no variability, it has expected value of 3.5 with variance of zero). Thanks,
Similar threads
