Binomial Distribution example - Chp. 3 (Quantitative Analysis)

[Raj Sachdeva]

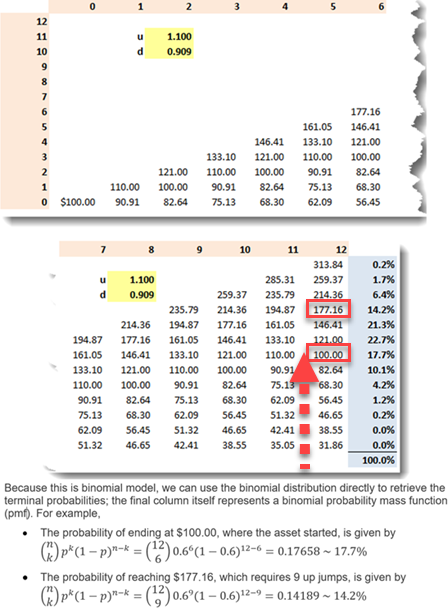
@David Harper CFA FRM - David, could you please explain how you arrived at values of k as 6 (prob. of ending at $100) and 9 (prob. of ending at $177.16)in following example noted in the Study notes (Chapter 3: Common Univariate Random Variables, pg.6)?

 

[David Harper CFA FRM]

Hi @Raj Sachdeva See below, please (your image plus minor annotation). I'm glad you asked because the very reason I included those bullets was to remind readers that each column in the binomial tree is itself a binomial distribution. (Yes, that's definitional if not tautological but I've noticed candidates often miss this feature). So if you look at the final column (i.e., 12 steps out) you will notice the thirteen values are unique and, if we start from the bottom, ascending; i.e., $31.86, 38.55, 46.65 ... Tuckman's notation for the bottommost value is node[12, 0] as in node[date = 12, state = 0]; 12 steps over, zero states up. The $100 is at node[date = 12, state = 6 steps up]; we can simply count from the bottom, 1, 2, 3, ... 5th is $82.64, 6th is $100, 7th is 121.00, 8th is 146.41, 9th is 177.16. The terminal value of $177.16 is nine states up, so its node is called n[12, 9]. Notation is aside, I just like to have notation to be able to reference ....

So the $100.00 is six states (vertical steps) "up from the bottom," and the $177.16 is nine states (vertical steps) up. As this tree recombines, it must requires six up jumps (and therefore six down) to reach the $100.00. Similarly, it must require 9 up jumps to reach the 177.16. In this way, this column (and every column) itself is a binomial distribution. I hope that's helpful,

 

[Raj Sachdeva]

@David Harper CFA FRM - thanks for the explanation David. It took me a little bit to make sense of this statement "As this tree recombines, it must requires six up jumps (and therefore six down) to reach the $100.00." but I think I got it eventually. I prepared the binomial tree to count the number of steps to 100 and came with 6 (using median as the starting point given equal number of up and down movements). The image may be useful to some readers so thought of putting it here. The concept works for $177.16 as well.