Backward Induction calculation

[flawless21]

Hi David! I was looking at your video labeled: Hull, Options, Futures & Other Derivatives, Chapter 13: Binomial Trees. Can you help me with your backward induction formulas. For a point of reference, please go to 28:34 of your lecture.

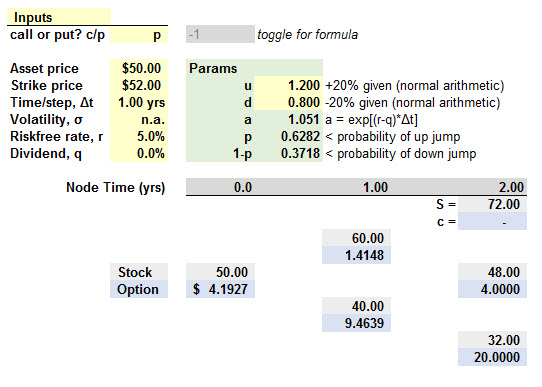
I understand all the numbers at the second node, its the discounting that is throwing me off.

Q1: For example, to get to 1.4148, I see that you do (4*.3718) which is 1.4872. 1.4872 * e(-1*.05) = 1.4146 which is what you have in node 1. Why are we using the probability of a down jump to calculate at node 1? We are calculating the probability of going from a price of 48 to 60 - therefore shouldn't it be P(up jump)? Or are we using .3718 because we are looking at a put value, and the probability of a down jump would be negative if the price went from 48->60?

Q2: I am unable to get 9.4639 or 4.1927. Can you please share your calculation? I would imagine regarding 9.4639, you would do (4*.6282) + (20*.3718) = 14.410. 14.410*e(-1*.05) = 13.70.

Q3: Can you explain again what the "a" (1.051) variable means in a binomial tree?

Thanks so much!

 

[David Harper CFA FRM]

Hi @omar72787 Sure, that's why we publish learning XLS, so you can see the concrete mechanics. Here is the corresponding sheet from our learning XLS: https://www.dropbox.com/s/hn6dskcmeahtih6/1108-hull-13-7.xlsx?dl=0 The example from the video, as labelled, is Hull's own Fig 13-7. Screenshot below.

1. The option value at node[1,1] =$1.4148 is the discounted expected value of the two nodes that are forward in time. If we assume that the path includes S[1,1] = $60.00 then the path is either up to $72.00 with probability (p) or down to $48.00 with probability (1-p). From the perspective of this node, the expected future value is the weighted probability p*0 + (1-p)*$4.00, but this must be discounted to the node [1,1] such that $1.4148 = [p*0 + (1-p)*$4.00]*exp(-rT) which symbolically is just something like [expected future value of the option weighted by probabilities p and (1-p)]*discounted to PV at node[1,1]. It's still an up jump from $60.00 to $72.00, but in the backward induction we are discounting the call option prices where in the "up jump" to $72.00, the option has zero value.
2. $9.4639 = (62.82%*$4.00 + 37.18%*$20.00)*exp(-5.0%*1.0 years). By the same logic of discounted expected value, $4.1927 = (62.82%*$1.4148 + 37.18%*$9.4639)*exp(-5.0%*1.0 years), where p = 62.82% and (1-p) = 37.18%
3. I am momentarily blanking (I have been on the forum all day and am a bit exhausted, it is not like me to forget! ). Somebody else posted a great intuition here on the forum about the (a) in the binomial, where I learned something, beyond the obvious (that it informs the p) I will see if i can find it tomorrow if that's okay? Thanks!

 

[flawless21]

You're the man David! Thank you. (I am assuming its okay if I am off by the fourth decimal point from you?)

 

[David Harper CFA FRM]

@omar72787 sure thing! re 4th decimal place difference, sorry I don't see which value, but sure that's a pretty small difference. The exhibit is from Excel, of course, where the values are rounded in display but accurate; eg, the more exact option value is
$4.1926543 but you wouldn't get that if you rounded the forward nodes, but no biggie. Thanks!