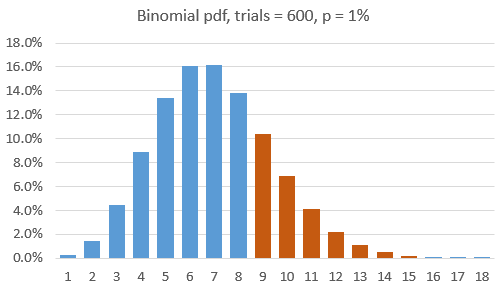
I `ve got a problem with Hull example. We back test a var with 600 data. The var confidence is 99% with nine exceptions. Expected number of exceptions is 6. Should we reject model? The probability of 9 or more exceptions is 0,152.Should we reject model at 5% significance level? Answer is no but I don`t understand it. Can somebody explain me when I should accept or reject model using binomial distribution?
Thanks.
Thanks.